Coordinate Geometry Class 9 Case Study Questions Maths Chapter 3

Q: Q8: How do you determine the quadrant of a point?

A8: The coordinate plane is divided into four quadrants: Quadrant I: Both x and y are positive. Quadrant II: x is negative, y is positive. Quadrant III: Both x and y are negative. Quadrant IV: x is positive, y is negative.

Download CBSE and ICSE Books in PDF Format

Reading Time: 7 minutes

Last Updated on October 26, 2024 by XAM CONTENT

Hello students, we are providing case study questions for class 9 maths. Case study questions are the new question format that is introduced in CBSE board. The resources for case study questions are very less. So, to help students we have created chapterwise case study questions for class 9 maths. In this article, you will find case study questions for CBSE Class 9 Maths Chapter 3 Coordinate Geometry. It is a part of Case Study Questions for CBSE Class 9 Maths Series.

Chapter	Coordinate Geometry
Type of Questions	Case Study Questions
Nature of Questions	Competency Based Questions
Board	CBSE
Class	9
Subject	Maths
Useful for	Class 9 Studying Students
Answers provided	Yes
Difficulty level	Mentioned
Important Link	Class 9 Maths Chapterwise Case Study

Customised Study Materials for Teachers, Schools and Coaching Institute

Table of Contents

Case Study Questions on Coordinate Geometry

Questions

Four friends Aakansha, Prabhat, Puneet and Lalit are sitting in a park at points A, B, C and D respectively. This park has been divided into small squares by drawing equally distanced horizontal and vertical lines. Consider XOX’ and YOY’ as coordinate axes.

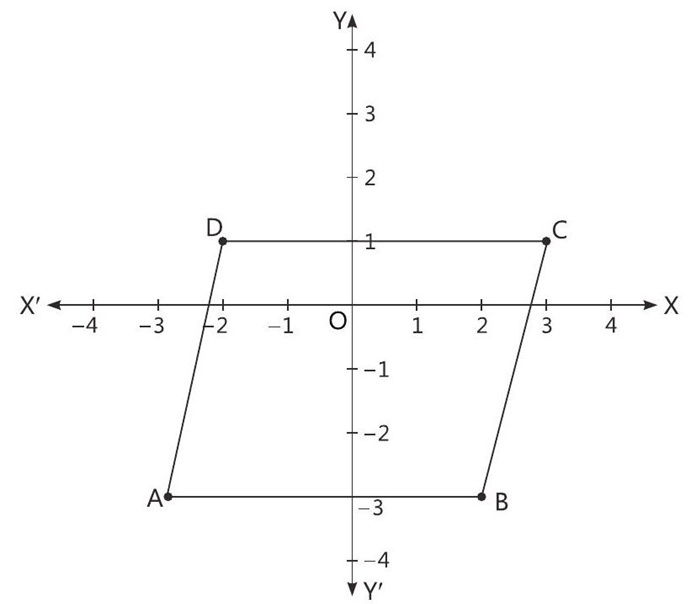
On the basis of the above information, solve the following questions:

Q. 1. Find the coordinates of B.

Q. 2. In which quadrant, point A is located?

Q. 3. Find the image of a point A with respect to Y-axis.

Q 4. Find the area of figure.

Solutions

Ans 1. The perpendicular distance of B from y is 2 in positive direction and perpendicular distance of B from X-axis is 3 in negative direction of Y-axis. Hence, coordinates of B are (2, -3).

Ans 2. Point A is located in III quadrant.

Ans 3. The coordinate of point A is (-3, 3). The image of a point A (-3, -3) with respect to Y-axis (3, -3).

Ans 4. Now, length of AB = |-3| + 2 = 3 + 2 = 5
Height = perpendicular distance of D from AB = 4
Therefore, Area of parallelogram = length x height = 5 x 4 = 20 sq. units.

Understanding Coordinate Geometry

Cartesian System: The system used to describe the position of a point in a plane. In this system, two mutually perpendicular lines are required, one is horizontal XOX’ called X-axis and the other is vertical YOY’ called Y-axis.
Cartesian Plane: The plane in cartesian system is called cartesian plane and the lines in it are called coordinate axes.
Origin: It is the point of intersection of the axes and is denoted by O. Its coordinates are (0, 0).
Quadrants: The coordinate-axes divide the plane into four parts called quadrants, numbered I, II, III and IV are in anti-clockwise from OX.

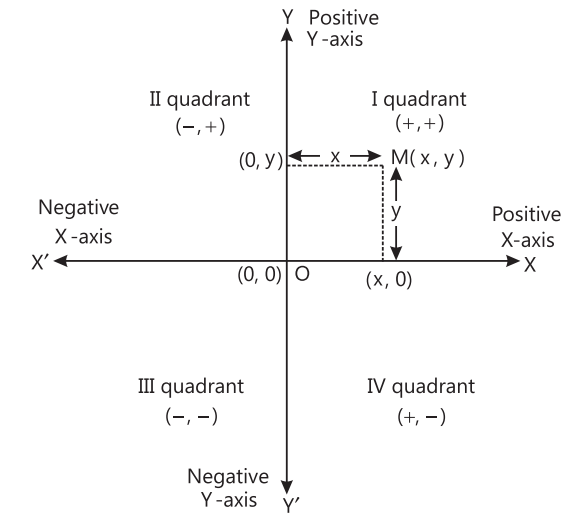
Coordinate Geometry Class 9 Case Study Questions Maths Chapter 3 - 2

Positive and Negative Directions:

The positive numbers lie in the directions OX and OY are said to be positive directions of X-axis and Y-axis respectively.
The negative numbers lie in the directions OX’ and OY’ are said to be negative directions of X-axis and Y-axis respectively.

Also check

Topics from which case study questions may be asked

The Cartesian plane
Coordinates of a point
Names and terms associated with the coordinate plane
Notations.

In stating the coordinates of a point in cartesian plane, the x-coordinate comes first and then the y-coordinate, We place the coordinates in brackets, i.e., (x, y)

Case study questions from the above given topic may be asked.

Helpful Links for CBSE Class 9 Preparation

Download Customised White Label Study Materials in MS Word Format

We are providing teaching resources to teachers and coaching institute looking for customised study materials in MS word format. Our High-quality editable study material which is prepared by the expert faculties are Highly useful for Teachers, Mentors, Tutors, Faculties, Coaching Institutes, Coaching Experts, Tuition Centers.

Download Product Brochure

Frequently Asked Questions (FAQs) on Coordinate Geometry Case Study

Q1: What is Coordinate Geometry?

A1: Coordinate Geometry, also known as analytic geometry, is the study of geometry using a coordinate system. This branch of mathematics uses algebraic equations to represent geometric shapes and analyze their properties, positions, and relationships in a two-dimensional plane.

Q2: What are the main concepts covered in Class 9 Coordinate Geometry?

A2: Class 9 Coordinate Geometry covers topics like the Cartesian coordinate system, plotting points on the coordinate plane, finding the distance between two points, and understanding the section formula.

Q3: What common mistakes should be avoided in Coordinate Geometry?

A3: Common mistakes include mis-plotting points on the coordinate plane, confusing the order of coordinates, incorrect application of formulas, and errors in arithmetic operations. It’s important to double-check your work and understand the underlying concepts to avoid these errors.

Q4: What is the Cartesian coordinate system?

A4: The Cartesian coordinate system is a two-dimensional plane defined by two perpendicular axes: the x-axis (horizontal) and the y-axis (vertical). The point where they intersect is called the origin, and each point on the plane is represented by a pair of coordinates (x, y).

Q5: How do you plot a point on the coordinate plane?

A5: To plot a point, first move along the x-axis to the x-coordinate, then move parallel to the y-axis to the y-coordinate. Mark the intersection of these positions on the plane.

Q6: What is the significance of the origin in Coordinate Geometry?

A6: The origin (0, 0) is the central point where the x-axis and y-axis intersect. It serves as the reference point for locating all other points on the plane.

Q8: How do you determine the quadrant of a point?

A8: The coordinate plane is divided into four quadrants:
Quadrant I: Both x and y are positive.
Quadrant II: x is negative, y is positive.
Quadrant III: Both x and y are negative.
Quadrant IV: x is positive, y is negative.

Q8: Are there any online resources or tools available for practicing coordinate geometry case study questions?

A8: We provide case study questions for CBSE Class 9 Maths on our website. Students can visit the website and practice sufficient case study questions and prepare for their exams. If you need more case study questions, then you can visit Physics Gurukul website. they are having a large collection of case study questions for all classes.