Last Updated on October 26, 2024 by XAM CONTENT
Hello students, we are providing case study questions for class 9 maths. Case study questions are the new question format that is introduced in CBSE board. The resources for case study questions are very less. So, to help students we have created chapterwise case study questions for class 9 maths. In this article, you will find case study questions for CBSE Class 9 Maths Chapter 1 Number Systems. It is a part of Case Study Questions for CBSE Class 9 Maths Series.
| Chapter | Number Systems |
| Type of Questions | Case Study Questions |
| Nature of Questions | Competency Based Questions |
| Board | CBSE |
| Class | 9 |
| Subject | Maths |
| Useful for | Class 9 Studying Students |
| Answers provided | Yes |
| Difficulty level | Mentioned |
| Important Link | Class 9 Maths Chapterwise Case Study |
Case Study Questions on Number Systems
Questions
Passage 1: Mrs. Rakhi lives in an undeveloped area where there is no facility of proper education. But one thing is available in that area i.e., network. Since she was very keen to take education, so she decided to complete her education through e-learning.
One day she was studying number system, where she learnt about rational numbers, irrational numbers and decimal numbers, etc.
On the basis of the above information, solve the following questions:
Q 1. Convert the rational number $\frac{2}{15}$ into decimal number.
Q 2. Write one irrational number between 2.365 and 3.125 .
Q 3. If $x+\sqrt{2}=3$, then find the value of $\frac{1}{x}$.
Q4. Find the product of two irrational numbers $(7+3 \sqrt{2})$ and $(7-3 \sqrt{2})$.
Difficulty Level: Medium
Solutions:
1.
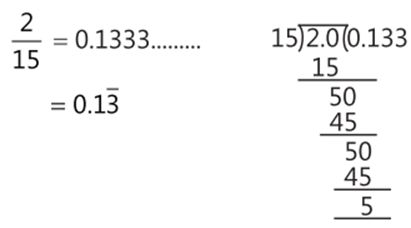
2. One irrational number between 2.365 and 3.125 is 2.6121121112 .
3. We have, $x+\sqrt{2}=3$
$$
\begin{aligned}
& : \frac{1}{x}=\frac{1}{3-\sqrt{2}} \times \frac{3+\sqrt{2}}{3+\sqrt{2}} \\
& \text { [by rationalisation] } \\
& =\frac{3+\sqrt{2}}{(3)^2-(\sqrt{2})^2} \\
& =\frac{3+\sqrt{2}}{9-2}=\frac{3+\sqrt{2}}{7}
\end{aligned}
$$
4. $(7+3 \sqrt{2})(7-3 \sqrt{2})=(7)^2-(3 \sqrt{2})^2$
$$
\begin{aligned}
& =49-18 \\
& =31
\end{aligned}
$$
Also check
- Statistics Class 9 Case Study Questions Maths Chapter 12
- Surface Areas and Volumes Class 9 Case Study Questions Maths Chapter 11
- Heron’s Formula Class 9 Case Study Questions Maths Chapter 10
- Circles Class 9 Case Study Questions Maths Chapter 9
- Quadrilaterals Class 9 Case Study Questions Maths Chapter 8
- Triangles Class 9 Case Study Questions Maths Chapter 7
- Lines and Angles Class 9 Case Study Questions Maths Chapter 6
- Introduction to Euclid’s Geometry Class 9 Case Study Questions Maths Chapter 5
- Linear Equations in Two Variables Class 9 Case Study Questions Maths Chapter 4
- Coordinate Geometry Class 9 Case Study Questions Maths Chapter 3
- Polynomials Class 9 Case Study Questions Maths Chapter 2
- Number Systems Class 9 Case Study Questions Maths Chapter 1
Topics from which case study questions may be asked
- Representation on number line
- Concept of rationalizing the denominator
- Rationalizing the denominator of expressions with square roots
- Applying the laws of exponents to simplify expressions
- Rationalizing surds
The sum or difference of a rational number and an irrational number is irrational.
The product or quotient of a non-zero rational number with an irrational number is irrational.
Case study questions from the above given topic may be asked.
Helpful Links for CBSE Class 9 Preparation
- Download Chapter Tests for CBSE Class 9 Science
- Download Important MCQ Questions for CBSE Class 9 Physics
- Download Worksheets for CBSE Class 9 Science
- Download Case Study Questions for CBSE Class 9 Maths
- Download Sample Papers for CBSE Class 9
- Download HOTS with Solutions for CBSE Class 9 Science
Download Customised White Label Study Materials in MS Word Format
We are providing teaching resources to teachers and coaching institute looking for customised study materials in MS word format. Our High-quality editable study material which is prepared by the expert faculties are Highly useful for Teachers, Mentors, Tutors, Faculties, Coaching Institutes, Coaching Experts, Tuition Centers.
Frequently Asked Questions (FAQs) on Number Systems Case Study
Q1: What is the significance of the number system in mathematics?
A1: The number system is fundamental in mathematics as it provides a systematic way to represent and work with numbers. It allows for the classification, comparison, and operation of numbers, which is essential for various mathematical concepts and real-world applications. Understanding the number system is crucial for solving problems in arithmetic, algebra, geometry, and beyond.
Q2: Are all integers also rational numbers?
A2: Yes, all integers are rational numbers because they can be expressed as a fraction where the denominator is 1. For example, 5 can be written as 5/1, making it a rational number.
Q3: How do you convert a repeating decimal into a fraction?
A3: To convert a repeating decimal into a fraction, you can set the repeating decimal as a variable and use algebraic manipulation.
For example,
for $x=0.666 \ldots$:
Let $x=0.666 \ldots$
Multiply both sides by 10 to shift the decimal point:
$10 x=6.666 \ldots$
Subtract the original equation from this new equation: $10 x-x=6.666 \ldots-0.666 \ldots$
Simplify: $9 x=6$
Solve for $x: x=\frac{6}{9}=\frac{2}{3}$
Q4: What are the key concepts covered in Chapter 1 of CBSE Class 9 Maths regarding number systems?
A4: Chapter 1 of CBSE Class 9 Maths covers concepts such as understanding rational numbers, irrational numbers and Laws of exponents.
(i) Review of representation of natural numbers and Integers on number line
(ii) Rational numbers on the number line.
(iii) Rational numbers as recurring/ terminating decimals
(iv) Operations on real numbers.
(v) Definition of nth root of a real number
(vi) Law of exponents with integral powers
Q5: What is the decimal expansion of rational numbers like?
A5: The decimal expansion of rational numbers is either terminating (e.g., 0.75) or non-terminating but repeating (e.g., 0.666… $=\frac{2}{3}$).
Q6: Can a number be both rational and irrational?
A6: No, a number cannot be both rational and irrational. A rational number can be expressed as a fraction of two integers, while an irrational number cannot. They are mutually exclusive categories.
Q7: Are there any online resources or tools available for practicing number systems case study questions?
A7: We provide case study questions for CBSE Class 9 Maths on our website. Students can visit the website and practice sufficient case study questions and prepare for their exams. If you need more case study questions, then you can visit Physics Gurukul website. they are having a large collection of case study questions for all classes.
Q8: What are the important keywords for CBSE Class 9 Maths Number Systems?
A8: List of important keywords given below –
Natural Numbers: Positive Counting number starting from 1.
Whole Number: All natural numbers together with 0.
Integers (Z): Set of all whole numbers and negative of natural numbers
Rational Number: Numbers which can be expressed in p/q form, where q ≠ 0 and p and q are integers.
Fraction: Numbers which can be expressed in form of p/q but are only positive
Equivalent Rational Numbers: Two rational numbers are said to be equivalent, if numerator and denominators of both rational numbers are in proportion or they are reducible to be equal.
