Circles Class 9 Case Study Questions Maths Chapter 9

Reading Time: 10 minutes

Last Updated on October 26, 2024 by XAM CONTENT

Hello students, we are providing case study questions for class 9 maths. Case study questions are the new question format that is introduced in CBSE board. The resources for case study questions are very less. So, to help students we have created chapterwise case study questions for class 9 maths. In this article, you will find case study questions for CBSE Class 9 Maths Chapter 9 Circles. It is a part of Case Study Questions for CBSE Class 9 Maths Series.

Chapter	Circles
Type of Questions	Case Study Questions
Nature of Questions	Competency Based Questions
Board	CBSE
Class	9
Subject	Maths
Useful for	Class 9 Studying Students
Answers provided	Yes
Difficulty level	Mentioned
Important Link	Class 9 Maths Chapterwise Case Study

Case Study Questions on Circles

Questions

Government of India is working regularly for the growth of handicapped persons. For these three STD booths situated at point P, Q and R are as shown in the figure, which are operated by handicapped persons. These three booths are equidistant from each other as shown in the figure.

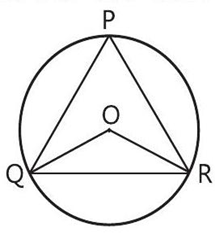
On the basis of the above information, solve the following questions:

Q. 1. Which type of ΔPQR in the given figure?

Q. 2. Measure angle ∠QOR.

Q. 3. Find the value of ∠OQR.

Q. 4. Is it true that points P, Q and R lie on the circle?

Solutions:

1. Given $P, Q$ and $R$ are equidistant. It means their distances are equal.

Note:
In an equilateral triangle, length of all three sides are equal.
So, $\triangle P Q R$ is an equilateral triangle.

2. Since, $\triangle P Q R$ is an equilateral triangle.

$$
\therefore \angle \mathrm{PQR}=\angle \mathrm{PRQ}=\angle \mathrm{QPR}=60^{\circ}
$$

The angle subtended by an arc at the centre is double the angle subtended by it any point on the remaining part of the circle.

$$
\therefore \angle Q O R=2 \angle Q P R=2 \times 60^{\circ}=120^{\circ}
$$

3. In $\triangle O Q R$,

$$
O Q=O R[\text { Radii of a circle })
$$

$\Rightarrow \angle \mathrm{ORQ}=\angle \mathrm{OQR}$ [Angles opposite to equal sides of a triangle are equal]
Using angle sum property of a triangle,

$$
\begin{aligned}
& \angle \mathrm{OQR}+\angle \mathrm{ORQ}+\angle \mathrm{QOR}=180^{\circ} \\
& \Rightarrow \angle \mathrm{OQR}+\angle \mathrm{OQR}+120^{\circ}=180^{\circ}
\end{aligned}
$$

$$
\begin{gathered}
\Rightarrow 2 \angle O Q R=60^{\circ} \\
\therefore \angle O Q R=30^{\circ}
\end{gathered}
$$

4. Yes, it is true that points $P, Q$ and $R$ lie on the circle.

Understanding Circles

Circle: A collection of all points in a plane which are at a constant distance from a fixed point. The fixed point is called the centre of the circle and the constant distance is called the radius.

In figure, O is the centre, OA is the radius and AB is the diameter of the circle.

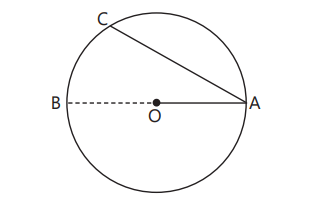
Chord: A line segment joining any two points on the circle. In figure, AC is the chord.

Diameter: Longest chord of the circle that passes through the centre of the circle.

Circumference: Length of the boundary of a circle.

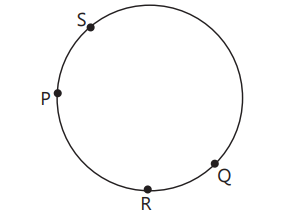
Arc: Any part of the circumference of a circle.

In figure, PRQ is minor arc represented as PRQ and PSQ is major arc represented as PSQ.

Semi-circle: Parts of a circle that are divided by its diameter.

Segment: The region between a chord and either of its arcs (major or minor). The segment formed with a minor arc is called minor segment and that formed with a major arc is called major segment.

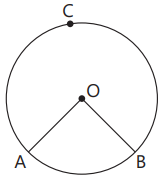
Sector: The region enclosed by an arc and the two radii joining the centre to the end points of the arc.

The sector corresponding to minor arc is called minor sector i.e., AOB and that corresponding to major arc is called major sector. i.e., AOBCA

Also check

• Statistics Class 9 Case Study Questions Maths Chapter 12
• Surface Areas and Volumes Class 9 Case Study Questions Maths Chapter 11
• Heron’s Formula Class 9 Case Study Questions Maths Chapter 10
• Circles Class 9 Case Study Questions Maths Chapter 9
• Quadrilaterals Class 9 Case Study Questions Maths Chapter 8
• Triangles Class 9 Case Study Questions Maths Chapter 7
• Lines and Angles Class 9 Case Study Questions Maths Chapter 6
• Introduction to Euclid’s Geometry Class 9 Case Study Questions Maths Chapter 5
• Linear Equations in Two Variables Class 9 Case Study Questions Maths Chapter 4
• Coordinate Geometry Class 9 Case Study Questions Maths Chapter 3
• Polynomials Class 9 Case Study Questions Maths Chapter 2
• Number Systems Class 9 Case Study Questions Maths Chapter 1

Topics from which case study questions may be asked

• Equal chords of a circle subtend equal angles at the center and (motivate) its converse.
• The perpendicular from the center of a circle to a chord bisects the chord and onversely, the line drawn through the center of a circle to bisect a chord is perpendicular to the chord.
• Equal chords of a circle (or of congruent circles) are equidistant from the center (or their respective centers) and conversely.
• The angle subtended by an arc at the center is double the angle subtended by it at any point on the remaining part of the circle.
• Angles in the same segment of a circle are equal.
• If a line segment joining two points subtends equal angle at two other points lying on the same side of the line containing the segment, the four points lie on a circle.
• The sum of either of the pair of the opposite angles of a cyclic quadrilateral is 180° and its converse.

Circles having same centre are called concentric circles.

Case study questions from the above given topic may be asked.

Helpful Links for CBSE Class 9 Preparation

• Download Chapter Tests for CBSE Class 9 Science
• Download Important MCQ Questions for CBSE Class 9 Physics
• Download Worksheets for CBSE Class 9 Science
• Download Case Study Questions for CBSE Class 9 Maths
• Download Sample Papers for CBSE Class 9
• Download HOTS with Solutions for CBSE Class 9 Science

Frequently Asked Questions (FAQs) on Circles Case Study