Lines and Angles Class 9 Case Study Questions Maths Chapter 6

By /
Reading Time: 9 minutes

Last Updated on November 15, 2024 by XAM CONTENT

Hello students, we are providing case study questions for class 9 maths. Case study questions are the new question format that is introduced in CBSE board. The resources for case study questions are very less. So, to help students we have created chapterwise case study questions for class 9 maths. In this article, you will find case study questions for CBSE Class 9 Maths Chapter 6 Lines and Angles. It is a part of Case Study Questions for CBSE Class 9 Maths Series.

ChapterLines and Angles
Type of QuestionsCase Study Questions
Nature of QuestionsCompetency Based Questions
BoardCBSE
Class9
SubjectMaths
Useful forClass 9 Studying Students
Answers providedYes
Difficulty levelMentioned
Important LinkClass 9 Maths Chapterwise Case Study

Case Study Questions on Lines and Angles

Questions

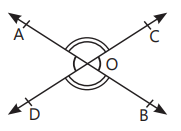
A math’s teacher was teaching students about intersecting lines.

Suppose AB and CD are two intersecting lines, which meets at point O. In this point O, she draw a line OE and all these lines were making different angles with each other.

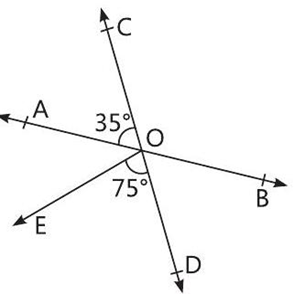
After explaining the description of the figure, she asked the following questions from the students.

On the basis of the above information, solve the following questions.

Q 1. Find the measure of ∠BOD.

Q 2. Check whether pair of angles ∠AOC and ∠BOC makes a linear pair.

Q 3. Which of the following angles form a non collinear lines?
(i) A, O, B
(ii) C, O, E

Q 4. Find the measure of ∠AOE.

Also read: Lines and Angles Class 9 Assertion Reason Questions

Solutions

1. From figure,

$$
\angle B O D=\angle A O C=35^{\circ}
$$

[Vertically opposite angles]

2. From figure, it is clear that

$$
\angle A O C+\angle B O C=180^{\circ}
$$

$[\because A B$ is a straight line $]$
Hence, $\angle A O C$ and $\angle B O C$ makes a linear pair.

3. (i) It is clear from the figure that points $A, O$ and $B$ form a collinear points.
(ii) It is clear from the figure that points $\mathrm{C}, \mathrm{O}, \mathrm{E}$ forms a non-collinear points.

Hence, points C, O, E form a non-collinear line.

4. From the given figure, $C D$ is a line segment.

Therefore, the sum of all angles of the same side of a line is $180^{\circ}$.

$$
\begin{aligned}
& \therefore \angle \mathrm{COA}+\angle \mathrm{AOE}+\angle \mathrm{EOD}=180^{\circ} \\
& \Rightarrow 35^{\circ}+\angle A O E+75^{\circ}=180^{\circ} \\
& \Rightarrow \angle \mathrm{AOE}=180^{\circ}-110^{\circ} \\
& =70^{\circ}
\end{aligned}
$$

Understanding Lines and Angles

Line: A geometrical object that is straight and extends indefinitely in both directions.
Line Segment: A part of a line with two end points.
Ray: A part of line with one end point.
Collinear Points: Three or more points lying on the same line are known as collinear points. Otherwise, they are non-collinear points.
Angle: It is formed when two rays originate from the same end point. The rays are called arms and the end point is called vertex.

Types of Angles:

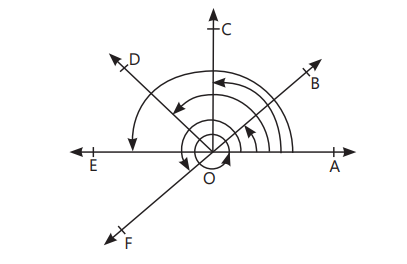
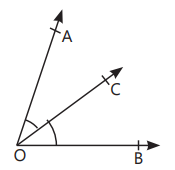
  1. Acute Angle: An angle with measure more than 0° but less than 90°. In figure, ∠AOB is acute angle.
  2. Obtuse Angle: An angle with measure more than 90° but less than 180°. In figure, ∠AOD is obtuse angle.
  3. Right Angle: An angle with measure exactly 90°. In figure, ∠AOC is right angle.
  4. Straight Angle: An angle with measure 180°. In figure, ∠AOE is straight angle.
  5. Reflex Angle: An angle with measure more than 180° but less than 360°. In figure, ∠AOF is reflex angle, when measured anticlockwise.
  6. Complete Angle: An angle with measure 360°. In figure, ∠AOA is complete angle.

Pair of Angles:

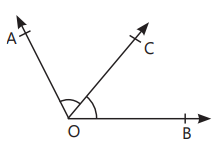
  1. Complementary Angles: Two angles with the sum of 90°. In above figure, ∠AOB + ∠BOC = 90°, so ∠AOB and ∠BOC are complementary angles.
  2. Supplementary Angles: Two angles with the sum of 180°. In above figure, ∠AOB + ∠BOE = 180°, so ∠AOB and ∠BOE are supplementary angles
  3. Adjacent Angles: Two angles having a common vertex and a common arm with uncommon arms on either side of the common arm. In figure, ∠AOC and ∠BOC are adjacent angles. OR When two angles are adjacent, then their sum is always equal to the angle formed by the two non-common arms. In figure, ∠AOB = ∠AOC + ∠BOC
  4. Linear Pair of Angles: Two adjacent angles with the sum of 180°. In figure, ∠AOC and ∠BOC are linear pair of angles.

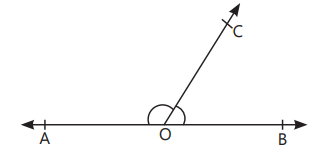
Vertically Opposite Angles: The pair of angles lying on the opposite sides of the point of intersection. In figure, (∠AOC and ∠BOD) and
(∠AOD and ∠BOC) are pairs of vertically opposite angles.

Bisector of an Angle: A ray which divides an angle into two equal parts.

Also check

Topics from which case study questions may be asked

  • Basic Terms and Definitions
  • Types of Angles
  • Intersecting Lines and Non-Intersecting Lines
  • Pairs of Angles
  • Parallel Lines and a Transversal
  • Angle Sum Property of a Triangle

The length of perpendiculars at different points on the parallel lines is same.

Case study questions from the above given topic may be asked.

Helpful Links for CBSE Class 9 Preparation

Download Customised White Label Study Materials in MS Word Format

We are providing teaching resources to teachers and coaching institute looking for customised study materials in MS word format. Our High-quality editable study material which is prepared by the expert faculties are Highly useful for Teachers, Mentors, Tutors, Faculties, Coaching Institutes, Coaching Experts, Tuition Centers.

Download Product Brochure

Frequently Asked Questions (FAQs) on Lines and Angles Case Study

Q1: What are the different types of angles?

A1: Angles are classified based on their measures:
Acute Angle: Measures less than 90°.
Right Angle: Measures exactly 90°.
Obtuse Angle: Measures more than 90° but less than 180°.
Straight Angle: Measures exactly 180°.
Reflex Angle: Measures more than 180° but less than 360°.

Q2: What are complementary and supplementary angles?

A2: Complementary Angles: Two angles are complementary if their sum is 90°.
Supplementary Angles: Two angles are supplementary if their sum is 180°.

Q3: What is a linear pair of angles?

A3: A linear pair of angles is formed when two adjacent angles add up to 180°. The angles in a linear pair are always supplementary.

Q4: What is the Angle Sum Property of a Triangle?

A4: The Angle Sum Property states that the sum of the interior angles of a triangle is always 180°.

Q5: What are parallel lines and a transversal?

A5: Parallel Lines: Two lines that are equidistant from each other and never intersect.
Transversal: A line that intersects two or more lines at distinct points. When a transversal cuts through parallel lines, it forms angles with specific relationships, like corresponding, alternate interior, and alternate exterior angles.

Q6: What is the significance of corresponding angles when a transversal intersects parallel lines?

A6: When a transversal intersects two parallel lines, the corresponding angles formed are equal. This property helps in proving that the lines are parallel and in solving various geometrical problems.

Q7: Are there any online resources or tools available for practicing Lines and Angles case study questions?

A8: We provide case study questions for CBSE Class 9 Maths on our website. Students can visit the website and practice sufficient case study questions and prepare for their exams. If you need more case study questions, then you can visit Physics Gurukul website. they are having a large collection of case study questions for all classes.

Lines and Angles Class 9 Case Study Questions Maths Chapter 6

Related Posts

CBSE eBooksICSE eBooks
Scroll to Top