Last Updated on December 13, 2024 by XAM CONTENT
Master the fundamentals of the Coordinate Geometry with our Class 9 Maths Chapter 3 notes, covering essential concepts, solved examples, and key points to help you excel in your exams
| Chapter | Coordinate Geometry |
| Type of Questions | Notes |
| Nature of Articles | Notes with examples |
| Board | CBSE |
| Class | 9 |
| Subject | Maths |
| Useful for | Class 9 Studying Students |
| Important Link | Class 9 Maths Chapterwise Notes |
Coordinate Geometry Notes
➤ Cartesian System: The system used to describe the position of a point in a plane. In this system, two mutually perpendicular lines are required, one is horizontal XOX’ called $X$-axis and the other is vertical YOY’ called $Y$-axis.
➤ Cartesian Plane: The plane in cartesian system is called cartesian plane and the lines in it are called coordinate axes.
➤ Origin: It is the point of intersection of the axes and is denoted by O. Its coordinates are $(0,0)$.
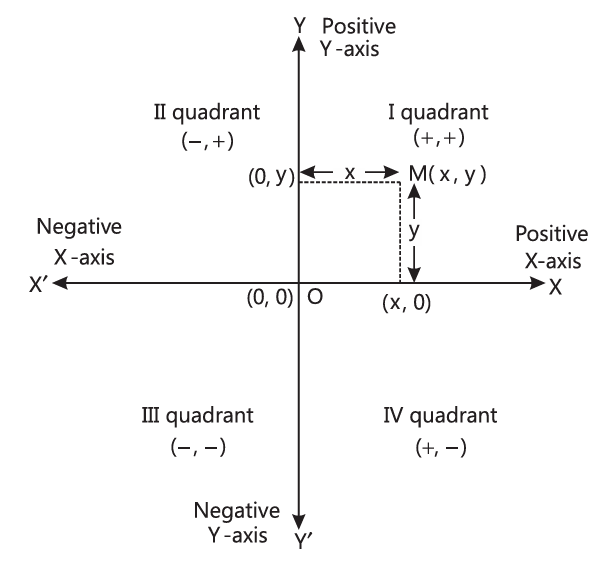
➤ Positive and Negative Directions:
1. The positive numbers lie in the directions $O X$ and OY are said to be positive directions of $X$-axis and $Y$-axis respectively.
2. The negative numbers lie in the directions OX’ and $\mathrm{OY}^{\prime}$ are said to be negative directions of $X$-axis and $Y$-axis respectively.
Things to Remember:
1. In stating the coordinates of a point in cartesian plane, the $x$-coordinate comes first and then the $y$-coordinate. We place the coordinates in brackets, i.e., ( $x, y)$.
2. The order of $x$ and $y$ is important in the coordinate $(x, y)$. So, $(x, y)$ is called an ordered pair.
3. Ordered pair $(x, y) \neq$ Ordered pair $(y, x)$, if $x \neq y$
4. Ordered pair $(x, y)=$ Ordered pair $(y, x)$, if $x=y$
5. The coordinates describe a point in the plane uniquely.
➤ Quadrants: The coordinate-axes divide the plane into four parts called quadrants, numbered I, II, III and IV are in anti-clockwise from OX.
The sign of these quadrants are I (,++ ), II (,-+ ), III (,–$)$ and IV (+,-).
➤ Coordinates of a Point: The coordinates of a point $M$ in the cartesian plane is represented by $M(x, y)$ where $x$ is abscissa and $y$ is ordinate.
1. Abscissa ( $x$-coordinate) = Perpendicular distance of a point from $Y$-axis.
2. Ordinate ( $y$-coordinate) = Perpendicular distance of a point from $X$-axis.
3. Coordinates of a point on $X$-axis are $(x, 0)$.
4. Coordinates of a point on $Y$-axis are $(0, y)$.
➤ Mirror Image of a Point: It is just a reflection of that point about the mirror. The image of different points under different mirrors are:

Also check
You may also like
| Case Study Questions Class 9 Maths | Case Study Questions Class 9 Science |
| Case Study Questions Class 9 SST | Assertion Reason Class 9 Science |
| Assertion Reason Class 9 Maths | Assertion Reason Class 9 SST |
Helpful Links for CBSE Class 9 Science Preparation
- Download Latest Sample Papers for CBSE Class 9 Science
- Download Worksheets for CBSE Class 9 Science
- Download Chapter Tests for CBSE Class 9 Science
- Download Case Study Question Bank for CBSE Class 9 Science
- Download Numerical Problems for CBSE Class 9 Physics
- Download Important MCQs for CBSE Class 9 Physics
Frequently Asked Questions (FAQs) on Coordinate Geometry Notes
Q1: What is Coordinate Geometry?
A1: Coordinate Geometry, also known as analytic geometry, is the study of geometry using a coordinate system. This branch of mathematics uses algebraic equations to represent geometric shapes and analyze their properties, positions, and relationships in a two-dimensional plane.
Q2: What are the main concepts covered in Class 9 Coordinate Geometry?
A2: Class 9 Coordinate Geometry covers topics like the Cartesian coordinate system, plotting points on the coordinate plane, finding the distance between two points, and understanding the section formula.
Q3: What common mistakes should be avoided in Coordinate Geometry?
A3: Common mistakes include mis-plotting points on the coordinate plane, confusing the order of coordinates, incorrect application of formulas, and errors in arithmetic operations. It’s important to double-check your work and understand the underlying concepts to avoid these errors.
Q4: What is the Cartesian coordinate system?
A4: The Cartesian coordinate system is a two-dimensional plane defined by two perpendicular axes: the x-axis (horizontal) and the y-axis (vertical). The point where they intersect is called the origin, and each point on the plane is represented by a pair of coordinates (x, y).
Q5: How do you plot a point on the coordinate plane?
A5: To plot a point, first move along the x-axis to the x-coordinate, then move parallel to the y-axis to the y-coordinate. Mark the intersection of these positions on the plane.
Q6: What is the significance of the origin in Coordinate Geometry?
A6: The origin (0, 0) is the central point where the x-axis and y-axis intersect. It serves as the reference point for locating all other points on the plane.
Q8: How do you determine the quadrant of a point?
A8: The coordinate plane is divided into four quadrants:
Quadrant I: Both x and y are positive.
Quadrant II: x is negative, y is positive.
Quadrant III: Both x and y are negative.
Quadrant IV: x is positive, y is negative.
Q8: Are there any online resources or tools available for practicing coordinate geometry case study questions?
A8: We provide case study questions for CBSE Class 9 Maths on our website. Students can visit the website and practice sufficient case study questions and prepare for their exams. If you need more case study questions, then you can visit Physics Gurukul website. they are having a large collection of case study questions for all classes.


