Quadrilaterals Class 9 Case Study Questions Maths Chapter 8

Download CBSE and ICSE Books in PDF Format

Reading Time: 9 minutes

Last Updated on October 26, 2024 by XAM CONTENT

Hello students, we are providing case study questions for class 9 maths. Case study questions are the new question format that is introduced in CBSE board. The resources for case study questions are very less. So, to help students we have created chapterwise case study questions for class 9 maths. In this article, you will find case study questions for CBSE Class 9 Maths Chapter 8 Quadrilaterals. It is a part of Case Study Questions for CBSE Class 9 Maths Series.

Chapter	Quadrilaterals
Type of Questions	Case Study Questions
Nature of Questions	Competency Based Questions
Board	CBSE
Class	9
Subject	Maths
Useful for	Class 9 Studying Students
Answers provided	Yes
Difficulty level	Mentioned
Important Link	Class 9 Maths Chapterwise Case Study

Customised Study Materials for Teachers, Schools and Coaching Institute

Table of Contents

Case Study Questions on Quadrilaterals

Questions

Due to frequent robberies in the colony during night. The secretary with the members together decides to attach more lights besides the street light set by municipality. There are poles on which lights are attached.

These 4 poles are connected to each other through wire and they form a quadrilateral. Light from pole B focus light on mid-point G of wire between pole C and B, from pole C focus light on mid-point F of wire between pole C and pole D. Similarly pole D and pole A focus light on the mid-point E and H respectively.

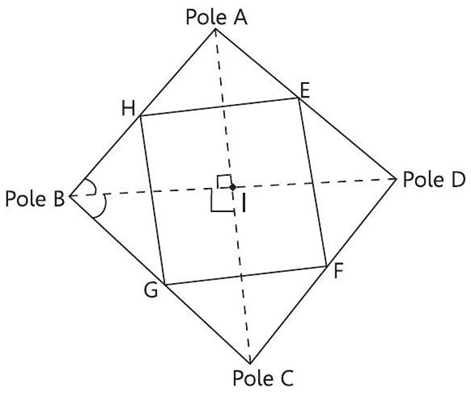
On the basis of the above information, solve the following questions:

Q 1. If BD is the bisector of ∠B then prove that I is the mid-point of AC.

Q 2. Prove that quadrilateral EFGH is a parallelogram.

Q 3. Is it true that every parallelogram is a rectangle?

Solutions

1. In $\triangle \mathrm{BIA}$ and $\triangle \mathrm{BIC}$,

$$
\begin{aligned}
\angle \mathrm{ABI} & =\angle \mathrm{CBI}[\mathrm{BD} \text { is a bisector of angle } \mathrm{B}] \\
\mathrm{BI} & =\mathrm{BI}[\mathrm{COmmon}] \\
\angle \mathrm{BIA} & =\angle \mathrm{BIC}[\text { Each } 90] \\
\therefore \triangle \mathrm{BIA} & \cong \Delta \mathrm{BIC}[\mathrm{SAS} \text { congruence rule }] \\
\therefore \mathrm{Al} & =\mathrm{Cl}[\mathrm{CPCT}]
\end{aligned}
$$
It means $I$ is the mid-point of $A C$. Hence proved

2. Here, $H G=\frac{1}{2} A C$ [By mid-point theorem] and
$E F=\frac{1}{2} \mathrm{AC}[$ By mid-point theorem $]$
$\mathrm{GH} \| \mathrm{EF}$ and $\mathrm{HG}=\mathrm{EF}$
If in a quadrilateral opposite side is parallel and equal then the quadrilateral is a parallelogram. So, quadrilateral EFGH is a parallelogram.

3. It is false, because every parallelogram is not a rectangle.

Understanding Quadrilaterals

Quadrilateral: A closed figure formed by four line segments (with no three points collinear). In quadrilateral PQRS; PQ, QR, RS and SP are sides; ∠P, ∠Q, ∠R and ∠S are the four angles; PR and QS are diagonals; Pairs (PQ, QR), (QR, RS), (RS, SP) and (SP, PQ) are adjacent sides; Pairs (∠Q, ∠S) and (∠P, ∠R) are of opposite angles. The sum of the four angles of a quadrilateral is 360°.

Parallelogram: A quadrilateral in which both opposite pairs of sides are parallel, is said to be parallelogram. In figure, ABCD is a parallelogram with AB || CD and BC || AD.

Properties of a Parallelogram:

(i) Opposite sides are equal and parallel.
(ii) Opposite angles are equal.
(iii) Diagonals bisect each other.
(iv) Diagonals divided it into two congruent triangles.
(v) The sum of the adjacent angles of a parallelogram is 180°.
(vi) If a pair of opposite sides is parallel and equal, then it is a parallelogram.

Mid-point Theorem: The line segment joining the mid-points of any two sides of a triangle is parallel to the third side and is equal to half of it.

Converse of Mid-point Theorem: The line drawn through the mid-point of one side of a triangle, parallel to another side bisects the third side.

Also check

Topics from which case study questions may be asked

Quadrilaterals
Parallelograms
Properties of a parallelogram
Mid-point theorem
Converse of Mid-point theorem

A trapezium is not a parallelogram (as only one pair of opposite sides is parallel in a trapezium and we require both pairs to be parallel in a parallelogram)

Case study questions from the above given topic may be asked.

Helpful Links for CBSE Class 9 Preparation

Download Customised White Label Study Materials in MS Word Format

We are providing teaching resources to teachers and coaching institute looking for customised study materials in MS word format. Our High-quality editable study material which is prepared by the expert faculties are Highly useful for Teachers, Mentors, Tutors, Faculties, Coaching Institutes, Coaching Experts, Tuition Centers.

Download Product Brochure

Frequently Asked Questions (FAQs) on Quadrilaterals Case Study

Q1: What is a quadrilateral?

A1: A quadrilateral is a polygon with four sides, four vertices, and four angles. The sum of the interior angles of any quadrilateral is always 360°.

Q2: What are the different types of quadrilaterals?

A2: Quadrilaterals can be classified into several types, including:
Parallelogram: Opposite sides are parallel and equal in length.
Rectangle: Opposite sides are parallel and equal in length, and all angles are 90°.
Square: All sides are equal, and all angles are 90°.
Rhombus: All sides are equal, but angles are not necessarily 90°.
Trapezium (Trapezoid): Only one pair of opposite sides is parallel.
Kite: Two pairs of adjacent sides are equal.

Q3: What is the significance of the diagonals in a parallelogram?

A3: In a parallelogram, the diagonals bisect each other. This means that each diagonal divides the parallelogram into two congruent triangles.

Q4: How do you prove that a quadrilateral is a parallelogram?

A4: A quadrilateral can be proved to be a parallelogram if any one of the following conditions is met:
(i) Both pairs of opposite sides are equal.
(ii) Both pairs of opposite angles are equal.
(iii) The diagonals bisect each other.
(iv) One pair of opposite sides is both parallel and equal.

Q5: What is the property of the angles in a cyclic quadrilateral?

A5: In a cyclic quadrilateral (a quadrilateral inscribed in a circle), the sum of the opposite angles is 180°. This property is known as the opposite angle theorem.

Q6: How can you prove that a quadrilateral is a rhombus?

A6: A quadrilateral can be proved to be a rhombus if any of the following conditions are satisfied:
All four sides are equal.
The diagonals bisect each other at right angles.
The diagonals bisect the angles of the quadrilateral.

Q7: What is the difference between a parallelogram and a rhombus?

A7: While both parallelograms and rhombuses have opposite sides that are parallel and equal, a rhombus has all four sides equal in length. Additionally, in a rhombus, the diagonals intersect at right angles, while in a parallelogram, they do not necessarily intersect at right angles.

Q8: How is the mid-point theorem related to quadrilaterals?

A8: The mid-point theorem states that the line segment joining the midpoints of two sides of a triangle is parallel to the third side and is half its length. This theorem is often used in problems related to quadrilaterals, particularly in proving properties of parallelograms.

Q9: Are there any online resources or tools available for practicing quadrilaterals case study questions?

A9: We provide case study questions for CBSE Class 9 Maths on our website. Students can visit the website and practice sufficient case study questions and prepare for their exams. If you need more case study questions, then you can visit Physics Gurukul website. they are having a large collection of case study questions for all classes.