Last Updated on October 31, 2024 by XAM CONTENT
Hello students, we are providing case study questions for class 9 maths. Case study questions are the new question format that is introduced in CBSE board. The resources for case study questions are very less. So, to help students we have created chapterwise case study questions for class 9 maths. In this article, you will find case study questions for CBSE Class 9 Maths Chapter 12 Statistics. It is a part of Case Study Questions for CBSE Class 9 Maths Series.
| Chapter | Statistics |
| Type of Questions | Case Study Questions |
| Nature of Questions | Competency Based Questions |
| Board | CBSE |
| Class | 9 |
| Subject | Maths |
| Useful for | Class 9 Studying Students |
| Answers provided | Yes |
| Difficulty level | Mentioned |
| Important Link | Class 9 Maths Chapterwise Case Study |
Case Study Questions on Statistics
Case Study Questions
Question 1:
India began its vaccination programmed on 16th January 2021. Within one year a massive population above 18 yr vaccinated upto 80% with double dose and 70% of children from age group 15 to 18 by taking 1st dose. This is all possible in short span of time due to combine efforts of governments and the citizens. The data collected by the government of vaccinated population is shown below.
| Ages | 15-20 | 20-25 | 25-30 | 30-35 |
| Number of peoples (in million) | 14 | 10 | 12 | 14 |
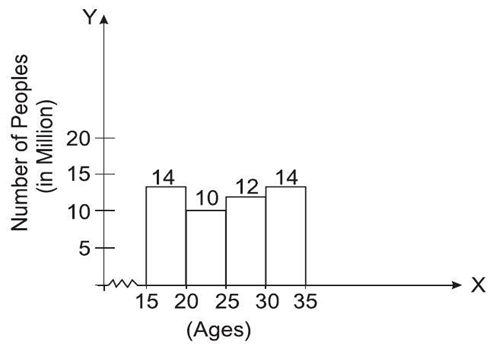
On the basis of the above information, solve the following questions.
Q 1. Upper limit of the fourth class interval is:
a. 30
b. 35
c. 35.5
d. 30.5
Q 2. The class mark of 3rd class interval is:
a. 27
b. 27.5
c. 28
d. 28.5
Q 3. The number of people having ages more than 25 is (in million):
a. 25
b. 26
c. 24
d. 23
Q 4. The number of peoples having maximum ages of 30 is (in million):
a. 36
b. 34
c. 33
d. 38
Q 5. In a histogram, the class intervals on the groups are taken along:
a. X-axis
b. Y-axis
c. Both a and b.
d. in between X and Y axes
Solutions:
(1) (b) In given data, the fourth class-interval is 30-35.
The upper limit of fourth class-interval 30-35 is 35.
So, option (b) is correct.
(2) (b) In a given data, the third class is 25-30.
$\therefore$ The class mark of $25-30$ is $\frac{25+30}{2}$
$$
=\frac{55}{2}=27.5
$$
So, option (b) is correct.
(3) (b) The number of peoples having ages more than 25 is 12+14 = 26 millions
So, option (b) is correct.
(4) (a) The number of peoples having maximum ages of 30 is 14+10+12 = 36 millions
So, option (a) is correct.
(5) (a) In a histogram, the class intervals or the groups are taken along X-axis.
Understanding Statistics
Statistics: Science of collection, organisation, presentation, analysis and interpretation of numerical data.
Data: Facts or figures that are numeral or otherwise collected with a definite purpose.
Range of Data: The difference of the highest and lowest observation in the given data.
Frequency: The number of occurrence (or repeated) of an observation.
Class-size or Class-width: The difference between the upper and lower class limits.
Class Mark: The mid value of class-interval.
Frequency Distribution: The table in which the corresponding frequencies are written against each class.
Inclusive or Discontinuous Frequency Distribution: A frequency distribution in which the upper limit of one class differs from the lower limit of the succeeding class e.g., in class-interval 0-10, 11-20, we include both 0 and 10.
Exclusive or Continuous Frequency Distribution: A frequency distribution in which the upper limit of one class coincides with the lower limit of the succeeding class e.g., in class-interval 0-10, 10-20, we include 0 and exclude 10.
Graphical Representation of Data: Representing the data through graphs:
(i) Bar Graph: Pictorial representation of data in which rectangular bars of uniform width are drawn with equal spacing between them on one axis usually the X-axis. The value of the variable is shown on other axis i.e., Y-axis.
(ii) Histogram: Graphical representation of frequency distribution of continuous variables in the form of vertical rectangles, where class intervals represented as bases and frequencies represented as heights.
Also check
- Statistics Class 9 Case Study Questions Maths Chapter 12
- Surface Areas and Volumes Class 9 Case Study Questions Maths Chapter 11
- Heron’s Formula Class 9 Case Study Questions Maths Chapter 10
- Circles Class 9 Case Study Questions Maths Chapter 9
- Quadrilaterals Class 9 Case Study Questions Maths Chapter 8
- Triangles Class 9 Case Study Questions Maths Chapter 7
- Lines and Angles Class 9 Case Study Questions Maths Chapter 6
- Introduction to Euclid’s Geometry Class 9 Case Study Questions Maths Chapter 5
- Linear Equations in Two Variables Class 9 Case Study Questions Maths Chapter 4
- Coordinate Geometry Class 9 Case Study Questions Maths Chapter 3
- Polynomials Class 9 Case Study Questions Maths Chapter 2
- Number Systems Class 9 Case Study Questions Maths Chapter 1
Topics from which case study questions may be asked
- Bar graphs
- Histograms (with varying base lengths), and
- Frequency polygons.
Statistics is the science of collection, organisation, presentation, analysis and interpretation of numerical data.
Case study questions from the above given topic may be asked.
Helpful Links for CBSE Class 9 Preparation
- Download Chapter Tests for CBSE Class 9 Science
- Download Important MCQ Questions for CBSE Class 9 Physics
- Download Worksheets for CBSE Class 9 Science
- Download Case Study Questions for CBSE Class 9 Maths
- Download Sample Papers for CBSE Class 9
- Download HOTS with Solutions for CBSE Class 9 Science
Download Customised White Label Study Materials in MS Word Format
We are providing teaching resources to teachers and coaching institute looking for customised study materials in MS word format. Our High-quality editable study material which is prepared by the expert faculties are Highly useful for Teachers, Mentors, Tutors, Faculties, Coaching Institutes, Coaching Experts, Tuition Centers.
Frequently Asked Questions (FAQs) on Statistics Case Study
Q1: What is Statistics in Maths?
A1: Statistics is a branch of mathematics dealing with data collection, analysis, interpretation, and presentation. In CBSE Class 9, students learn how to organize and analyze data using tables, graphs, and other techniques to draw meaningful conclusions.
Q2: What are the types of data in statistics?
A2: Data in statistics is generally classified as:
Primary Data: Data collected directly from an experiment, survey, or observation.
Secondary Data: Data obtained from published sources or previously collected data.
Q3: What is the difference between a bar graph and a histogram?
A3: Bar Graph: Used to represent categorical data with rectangular bars. Each bar’s length represents the frequency of a category, and bars are usually separated by spaces.
Histogram: Used to represent continuous data with adjacent bars, showing the frequency of intervals (or classes) of a continuous variable. In a histogram, bars touch each other.
Q4: How do you calculate the mean of a data set?
A4: The mean of a data set is calculated by adding all the observations together and dividing by the total number of observations.
Q5: What is a frequency distribution table, and why is it useful?
A5: A frequency distribution table organizes raw data into different classes or intervals to show the frequency (number of occurrences) of each interval. It helps in understanding data patterns and simplifying complex data for easier interpretation.
Q6: What is cumulative frequency, and how is it different from frequency?
A6: Frequency refers to the number of times a specific value or class appears in a data set.
Cumulative Frequency is the sum of frequencies accumulated up to a particular class or value. It helps in determining how many data points fall below a certain class interval.
Q7: What is the purpose of the median in statistics?
A7: The median is the middle value in a data set when arranged in ascending or descending order. It is useful in understanding the central tendency of data, especially when there are outliers that might skew the mean.
Q8: What is the purpose of the median in statistics?
A8: Common mistakes include:
Using incorrect formulas for specific shapes.
Forgetting to square or cube units correctly.
Mixing up radius and diameter (especially with spheres and cylinders).
Not including all surfaces in total surface area calculations, such as forgetting the circular bases in cylinders.
Q9: Are there any online resources or tools available for practicing statistics case study questions?
A9: We provide case study questions for CBSE Class 9 Maths on our website. Students can visit the website and practice sufficient case study questions and prepare for their exams. If you need more case study questions, then you can visit Physics Gurukul website. they are having a large collection of case study questions for all classes.
