Heron's Formula Class 9 Case Study Questions Maths Chapter 10

Download CBSE and ICSE Books in PDF Format

Reading Time: 8 minutes

Last Updated on October 26, 2024 by XAM CONTENT

Hello students, we are providing case study questions for class 9 maths. Case study questions are the new question format that is introduced in CBSE board. The resources for case study questions are very less. So, to help students we have created chapterwise case study questions for class 9 maths. In this article, you will find case study questions for CBSE Class 9 Maths Chapter 10 Heron’s Formula. It is a part of Case Study Questions for CBSE Class 9 Maths Series.

Chapter	Heron’s Formula
Type of Questions	Case Study Questions
Nature of Questions	Competency Based Questions
Board	CBSE
Class	9
Subject	Maths
Useful for	Class 9 Studying Students
Answers provided	Yes
Difficulty level	Mentioned
Important Link	Class 9 Maths Chapterwise Case Study

Customised Study Materials for Teachers, Schools and Coaching Institute

Table of Contents

Case Study Questions on Heron’s Formula

Questions

Mayank bought a triangle shape field and wants to grow potato and wheat on his field. He divided his field by joining opposite sides. On the largest park he grew wheat and on the rest part he grew potato. The dimensions of a park are shown in the park.

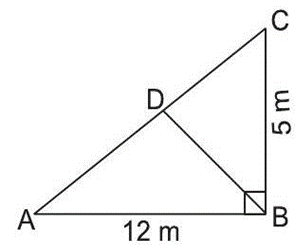
On the basis of the above information, solve the following questions:

Q 1. Find the length of AC in ΔABC.

Q 2. Find the area of ΔABC.

Q 3. If the cost of ploughing park is ₹5 per cm², then find the total cost of ploughing the park.

Solutions:

1. In right angled $\triangle A B C$, use Pythagoras theorem,

$$
\begin{aligned}
A C & =\sqrt{(A B)^2+(B C)^2}=\sqrt{(12)^2+(5)^2} \\
\vdots & =\sqrt{144+25}=\sqrt{169}=13 \mathrm{~m}
\end{aligned}
$$

Hence, length of $A C$ is 13 m .

2. Area of $\triangle \mathrm{ABC}$

$$
\begin{aligned}
& =\frac{1}{2} \times A B \times B C \\
& =\frac{1}{2} \times 12 \times 5=30 \mathrm{~m}^2
\end{aligned}
$$

3. Since, the total area of the park $=30 \mathrm{~m}^2$
$\because$ The cost of ploughing the park in $1 \mathrm{~m}^2=5$
$\therefore$ The cost of ploughing the park in $30 \mathrm{~m}^2$

$$
\begin{aligned}
& = 5\times 30\\
& =150
\end{aligned}
$$

Understanding Heron’s Formula

Area of Triangle: The total space occupied inside the boundary of the triangle is said to be an area of triangle.

Perimeter of Triangle: Sum of lengths of all three sides of a triangle.

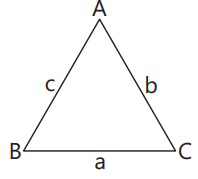
Perimeter,

$\begin{aligned} 2 s & =a+b+c \\ s & =\frac{a+b+c}{2}\end{aligned}$

Right-angled Triangle: It is a triangle with one right angle.

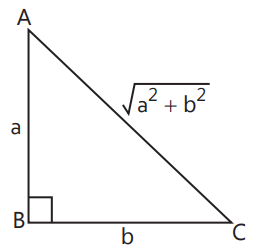
1. Area $=\frac{1}{2} \times a \times b$
2. Altitude $=a$
3. Perimeter$=a+b+\sqrt{a^2+b^2}$

where ‘a’ and ‘b’ are the sides that includes to the right angle.

Isosceles Triangle: Triangle that has two equal sides and corresponding two equal angles.

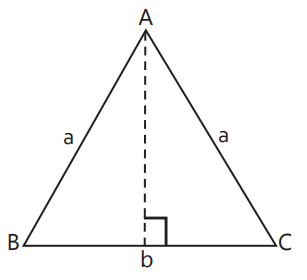
1. Area $=\frac{b}{4} \sqrt{4 a^2-b^2}$
2. Perimeter $=2 a+b$
3. Altitude $=\frac{1}{2} \sqrt{4 a^2-b^2}$

where ‘a’ is length of two equal sides and ‘b’ is base.

Equilateral Triangle: Triangle with all sides and all angles equal (each being 60°)

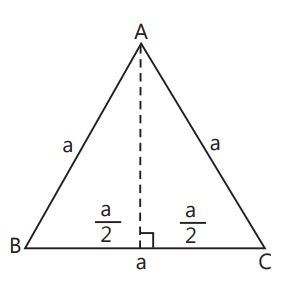
1. Area $=\frac{\sqrt{3}}{4} a^2$
2. Perimeter $=3 a$
3. Altitude $=\frac{\sqrt{3}}{2} a$

where ‘a’ is side.

Heron‘s Formula: The formula given by Heron about the area of a triangle.

Area of triangle $=\sqrt{s(s-a)(s-b)(s-c)}$

where a, b and c are the sides of triangle and s is its semi-perimeter.

Boost your knowledge

(i) The length of longest altitude is the perpendicular distance from the opposite vertex to the smallest side of a triangle.
(ii) The length of smallest altitude is the perpendicular distance from the opposite vertex to the largest side of a triangle.
(iii) Heron‘s formula is helpful when it is not possible to find the height of the triangle easily.
(iv) Heron‘s formula is applicable to all types of triangles whether it is a right triangle or an isosceles or an equilateral triangle

Download Class 9 Sample Papers

Also check

Topics from which case study questions may be asked

Quadrilaterals
Parallelograms
Properties of a parallelogram
Mid-point theorem
Converse of Mid-point theorem

A trapezium is not a parallelogram (as only one pair of opposite sides is parallel in a trapezium and we require both pairs to be parallel in a parallelogram)

Case study questions from the above given topic may be asked.

Helpful Links for CBSE Class 9 Preparation

Download Customised White Label Study Materials in MS Word Format

We are providing teaching resources to teachers and coaching institute looking for customised study materials in MS word format. Our High-quality editable study material which is prepared by the expert faculties are Highly useful for Teachers, Mentors, Tutors, Faculties, Coaching Institutes, Coaching Experts, Tuition Centers.

Download Product Brochure

Frequently Asked Questions (FAQs) on Heron’s Formula Case Study

Q1: What is Heron’s Formula?

A1: Heron’s Formula is used to calculate the area of a triangle when the lengths of all three sides are known. The formula is:
Area of triangle $=\sqrt{s(s-a)(s-b)(s-c)}$

Q2: How is Heron’s Formula derived?

A2: Heron’s formula is derived from the general area formula of a triangle. It simplifies the calculation of the area without needing the height. This is particularly useful for triangles where the height is difficult to determine directly. The formula is based on the triangle’s semi-perimeter and each of its sides.

Q3: When should Heron’s Formula be used?

A3: Heron’s Formula should be used when the lengths of all three sides of a triangle are given, and the height is unknown. It allows you to find the area of any triangle (scalene, isosceles, or equilateral) as long as you know the sides.

Q4: Can Heron’s Formula be used for right-angled triangles?

A4: Yes, Heron’s Formula can be used for right-angled triangles, although for right-angled triangles, a simpler method involving the base and height (half the product of the base and height) can also be used to find the area.

Q5: What is the significance of the semi-perimeter in Heron’s Formula?

A5: The semi-perimeter (s) is half the perimeter of the triangle. It acts as a key variable in the formula, simplifying the calculation of the area by incorporating all three sides of the triangle in a single expression.

Q6: Can Heron’s Formula be applied to a quadrilateral?

A6: No, Heron’s Formula specifically applies to triangles. However, if a quadrilateral can be divided into two triangles, the area of each triangle can be found using Heron’s Formula, and the sum of the areas will give the total area of the quadrilateral.

Q7: How is Heron’s Formula applied in real-life problems?

A7: Heron’s Formula is used in fields like civil engineering, architecture, and land surveying where determining the area of irregular land plots or structures is necessary, especially when only the lengths of the boundaries are known.

Q8: Are there any online resources or tools available for practicing Circles case study questions?

A9: We provide case study questions for CBSE Class 9 Maths on our website. Students can visit the website and practice sufficient case study questions and prepare for their exams. If you need more case study questions, then you can visit Physics Gurukul website. they are having a large collection of case study questions for all classes.