Last Updated on December 14, 2024 by XAM CONTENT
Hello students, we are providing case study questions for class 6 maths. Case study questions are the new question format that is introduced in CBSE board. The resources for case study questions are very less. So, to help students we have created chapterwise case study questions for class 6 maths. In this article, you will find case study questions for CBSE Class 8 Maths Chapter 10 The Other Side of Zero. It is a part of Case Study Questions for CBSE Class 6 Maths Series.
| Chapter | The Other Side of Zero |
| Type of Questions | Case Study Questions |
| Nature of Questions | Competency Based Questions |
| Board | CBSE |
| Class | 6 |
| Subject | Maths |
| Useful for | Class 6 Studying Students |
| Answers provided | Yes |
| Difficulty level | Mentioned |
| Important Link | Class 6 Maths Chapterwise Case Study |
Case Study Questions on The Other Side of Zero
Questions
The figure shows the position of the satellite above earth.
PR is the line joining the satellite and the centre of earth. P is the position of the satellite; Q is a point on the surface of earth and R is the centre of earth.
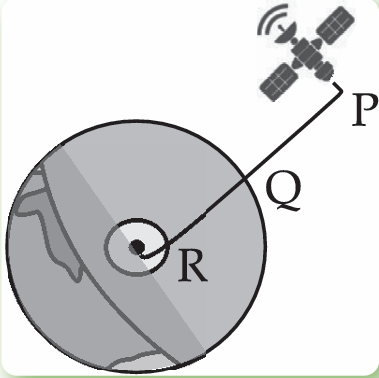
The distance between P and Q is 1300 km and the distance between the centre of earth and the satellite is 7617 km.
Q. 1. What is the distance between the points Q and R?
(a) 1300 km
(b) 6371 km
(c) 7671 km
(d) 8971 km
Ans. Option (b) is correct.
Explanation: 6371 km (7671 – 1300)
Q. 2. Shobhit marks Q as zero and the direction from Q to P is positive. What is the distance of R with reference to P?
Sol. 7671 km
Q. 3. What is the opposite of the sentence ‘ Ascending to a height of 6000 km’?
Sol. Its opposite is ‘descending to a height of 6000 km.’
Q. 4. If point Q is taken as zero, then write 1050 km inside the earth surface or towards P in form of integers?
Sol. – 1050 km
Q. 5. 8 – 8 = 0 Which of the following is true for the numbers shown above?
(a) –8 is a multiplicative inverse of 8.
(b) –8 is a multiplicative identity of 8.
(c) –8 is the additive identity of 8.
(d) –8 is the additive inverse of 8.
Sol. Option (d) is correct.
Explanation: 8 + (– 8) = 0
Topics from which case study questions may be asked
- Integers
- Additive Inverse of a Number
- Representation of Integers on a Number Line
- Ordering of Integers
- Addition of Integers on a Number Line
- Addition of Integers
- Subtraction of Integers Using Number Line
- Subtraction of Integers
- General Rules about Addition and Subtraction of Integers
Case study questions from the above given topic may be asked.
Learning Objectives
- Integers include zero, positive and negative numbers.
- Integers can be represented on a number line.
- Integers can be arranged in ascending and descending order.
- Addition and subtraction of integers follows certain rules. This can also be represented using a number line.
Understanding The Other Side of Zero
- Negative numbers go below zero on the number line.
- The collection of numbers…, – 4, – 3, – 2, – 1, 0, 1, 2, 3, 4, … is called integers.
- – 1, – 2, – 3, – 4, … called negative numbers are negative integers and 1, 2, 3, 4, … called positive numbers are the positive integers.
- Integers can be represented on a number line with zero in the middle, positive numbers on the right and negative numbers on the left.
- One more than given integer gives the successor and one less than given integer gives the predecessor.
- When two positive integers are added, we get a positive integer.
- When two negative integers are added, we get a negative integer.
- When one positive and one negative integer is added we subtract them as whole numbers by considering the numbers without their sign and then put the sign of the bigger number with the difference obtained.
- Addition and subtraction of integers can also be shown on a number line.
Integers are whole numbers that can be positive, negative, or zero, without fractional or decimal parts.
Frequently Asked Questions (FAQs) on The Other Side of Zero Case Study
Q1: What does “The Other Side of Zero” mean in mathematics?
A1: “The Other Side of Zero” refers to negative numbers, which lie on the left side of zero on a number line. These numbers represent values less than zero, often used to describe situations like debts, temperatures below freezing, or elevations below sea level.
Q2: What are negative numbers?
A2: Negative numbers are numbers less than zero, represented with a minus sign (-).
Example: -3, -7, -12.
Q3: How are negative numbers represented on a number line?
A3: Negative numbers are placed to the left of zero on a number line, with smaller negative numbers (like −1) closer to zero and larger negative numbers (like −10) farther away.
Q4: What is the difference between positive and negative numbers?
A4: Positive Numbers: Numbers greater than zero, located to the right of zero on the number line.
Negative Numbers: Numbers less than zero, located to the left of zero on the number line.
Q5: What is zero, and is it positive or negative?
A5: Zero is a neutral number that separates positive and negative numbers on a number line. It is neither positive nor negative.
Q6: How do we compare positive and negative numbers?
A6: Positive numbers are always greater than negative numbers. Example: 5 > −3.
Among negative numbers, the number closer to zero is greater. Example: -2 > −5.
Q7: What are the rules for adding positive and negative numbers?
A7: Adding two positive numbers: Add their values. Example: 3+5=8.
Adding two negative numbers: Add their values and keep the negative sign. Example: −3+(−5) = −8.
Adding a positive and a negative number: Subtract their values and take the sign of the larger number. Example: 3+(-5) = -2 and −3+5=2.
Q8: What are some real-life examples of negative numbers?
A8: Negative numbers are used in situations like:
Temperatures: −5∘C indicates 5 degrees below zero.
Money: A bank balance of −$100 indicates a debt of $100.
Altitude: An elevation of −20 meters indicate 20 meters below sea level.
Q9: Can zero have a negative counterpart?
A9: No, zero does not have a positive or negative counterpart. It is a neutral number and the starting point on a number line.
Q10: How do you multiply and divide positive and negative numbers?
A10: Multiplication Rules:
Positive × Positive = Positive.
Negative × Negative = Positive.
Positive × Negative = Negative.
Division Rules:
Positive ÷ Positive = Positive.
Negative ÷ Negative = Positive.
Positive ÷ Negative = Negative.
Q11: What happens when you add zero to a negative or positive number?
A11: Adding zero to any number does not change its value.
Q12: Can negative numbers be fractions or decimals?
A12: Yes, negative numbers can also be fractions or decimals.
Q13: What is the absolute value of a number?
A13: The absolute value of a number is its distance from zero on the number line, ignoring the sign.
Q14: Are there any online resources or tools available for practicing “The Other Side of Zero” case study questions?
A14: We provide case study questions for CBSE Class 6 Maths on our website. Students can visit the website and practice sufficient case study questions and prepare for their exams. If you need more case study questions, then you can visit Physics Gurukul website. they are having a large collection of case study questions for all classes.
