Last Updated on April 29, 2025 by XAM CONTENT
Hello students, we are providing case study questions for class 8 maths. Case study questions are the new question format that is introduced in CBSE board. The resources for case study questions are very less. So, to help students we have created chapterwise case study questions for class 8 maths. In this article, you will find case study questions for CBSE Class 8 Maths Chapter 3 Understanding Quadrilaterals. It is a part of Case Study Questions for CBSE Class 8 Maths Series.
| Chapter | Understanding Quadrilaterals |
| Type of Questions | Case Study Questions |
| Nature of Questions | Competency Based Questions |
| Board | CBSE |
| Class | 8 |
| Subject | Maths |
| Useful for | Class 8 Studying Students |
| Answers provided | Yes |
| Difficulty level | Mentioned |
| Important Link | Class 8 Maths Chapterwise Case Study |
Case Study Questions on Understanding Quadrilaterals
Questions
There is a trapezium MNOP, angle bisector of ∠M and ∠N meet at point W, and angle bisector of ∠O and ∠P meet at point X on side MN of trapezium MNOP.
By using the figure give the answers to following questions:
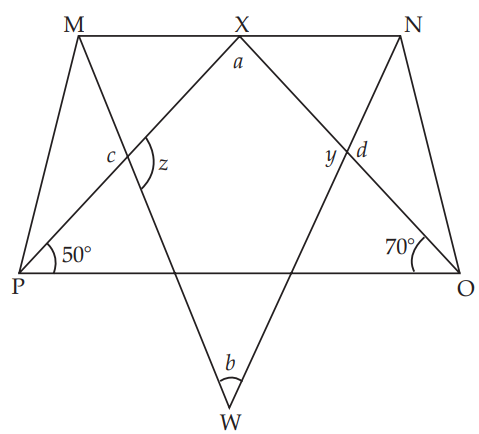
Q. 1. What is the value of a?
(a) 80°
(b) 60°
(c) 90°
(d) 70°
Ans. Option (b) is correct.
Explanation: In Triangle XPO, ∠XPO = 50°
(XP is angle bisector of ∠X)
∠XOP = 70° (XO is angle bisector of ∠XPO)
∠XOP + ∠XPO + a = 180°
70° + 50° + a = 180°
a = 180°– 120°
a = 60°
Q. 2. What is the value of d?
(a) 70°
(b) 60°
(c) 80°
(d) 90°
Ans. Option (d) is correct.
Explanation: ∠O + ∠N = 180°
(sum of adjacent angles of trapezium is 180°)
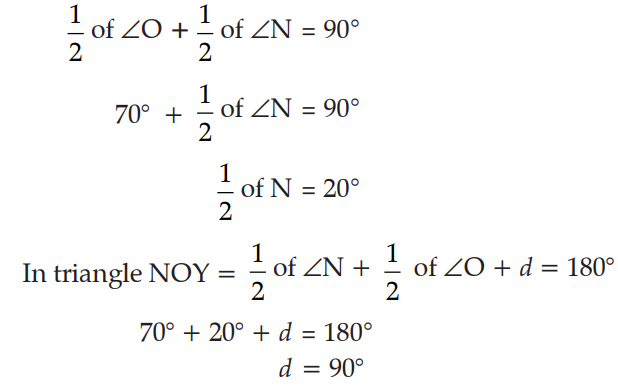
Also read: Understanding Quadrilaterals Assertion Reason Questions for Class 8
Q. 3. What is the value of c?
(a) 90°
(b) 70°
(c) 50°
(d) 80°
Ans. Option (a) is correct.
Explanation: ∠P + ∠M = 180°
(sum of adjacent angles of trapezium is 180°)
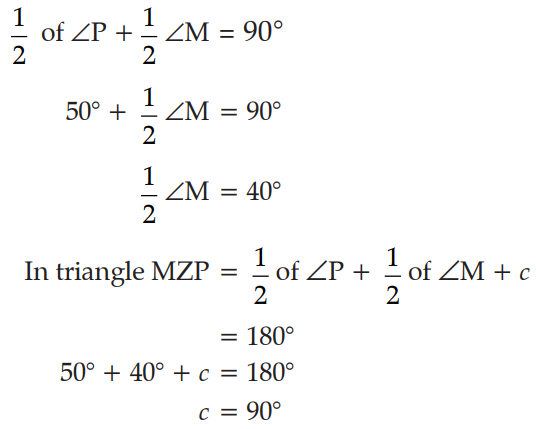
Q. 4. What type of triangle is POX?
Ans. In triangle POX,
All angles are less than 90°, therefore it is an acute angle triangle.
Q. 5. What is the value of b?
Ans. In quadrilateral XYWZ,
a + b + y +z = 360°
c = y = 90° (vertically opposite angles are equal)
d = z = 90° (vertically opposite angles are equal)
60° + b + 90°+ 90° = 360°
b = 120°

Also check
- Introduction to Graphs Class 8 Case Study Questions Maths Chapter 13
- Factorisation Class 8 Case Study Questions Maths Chapter 12
- Direct and Inverse Proportions Class 8 Case Study Questions Maths Chapter 11
- Exponents and Powers Class 8 Case Study Questions Maths Chapter 10
- Mensuration Class 8 Case Study Questions Maths Chapter 9
- Algebraic Expressions and Identities Class 8 Case Study Questions Maths Chapter 8
- Comparing Quantities Class 8 Case Study Questions Maths Chapter 7
- Cube and Cube Roots Class 8 Case Study Questions Maths Chapter 6
- Square and Square Roots Class 8 Case Study Questions Maths Chapter 5
- Data Handling Class 8 Case Study Questions Maths Chapter 4
- Understanding Quadrilaterals Class 8 Case Study Questions Maths Chapter 3
- Linear Equations in One Variable Class 8 Case Study Questions Maths Chapter 2
- Rational Numbers Class 8 Case Study Questions Maths Chapter 1
🚀 Boost Your Exam Prep: Get case study questions for all subjects (Class 6-12) now!
👉 Explore more resources on CBSE Class 8
Download eBooks for CBSE Class 8 Maths Understanding Quadrilaterals
Download eBooks for CBSE Class 8 Maths
- Rational Numbers Topicwise Worksheet for CBSE Class 8 Maths
- Linear Equations in One Variable Worksheet for CBSE Class 8 Maths
- Understanding Quadrilaterals Worksheet for CBSE Class 8 Maths
- Data Handling Worksheet for CBSE Class 8 Maths
- Squares and Square Roots Worksheet for CBSE Class 8 Maths
- Cube and Cube Roots Worksheet for CBSE Class 8 Maths
- Comparing Quantities Worksheet for CBSE Class 8 Maths
- Algebraic Expressions and Identities Worksheet for CBSE Class 8 Maths
Topics from which case study questions may be asked
- Convex and Concave Polygons.
- Regular and Irregular Polygons.
- Sum of Measures of the Exterior Angles of a Polygon.
- Kinds of QuadrilateralTrapezium; Kite; Parallelogram.
- Some Special ParallelogramsRhombus; Rectangle; Square.
Frequently Asked Questions (FAQs) on Understanding Quadrilaterals Case Study
Q1: Why understanding quadrilaterals are important?
A1: Understanding quadrilaterals is crucial for building a strong foundation in geometry, enabling real-world applications in design and construction. It enhances problem-solving skills, fosters critical thinking, and prepares students for advanced mathematical concepts and career opportunities.
Q2: What is a quadrilateral?
A2: A quadrilateral is a polygon with four sides and four angles.
Q3: What are the different types of quadrilaterals?
A3: There are various types of quadrilaterals, including squares, rectangles, parallelograms, rhombuses, trapeziums, and kites.
Q4: How do you classify quadrilaterals based on their properties?
A4: Quadrilaterals can be classified based on their properties such as sides, angles, and diagonals.
For example:
(1) Parallelograms have opposite sides that are equal and parallel.
(2) Rhombuses have all four sides equal in length.
(3) Rectangles have all angles equal to 90 degrees.
Q5: What is the sum of angles in a quadrilateral?
A5: The sum of angles in any quadrilateral is always 360 degrees.
Q6: Can a quadrilateral have equal sides and angles but still not be a square?
A6: Yes, a rhombus can have all sides equal and opposite angles equal, but its angles need not be right angles, unlike in a square.
Q7: How do you prove that a quadrilateral is a parallelogram?
A7: A quadrilateral can be proved as a parallelogram if its opposite sides are equal and parallel, or if its opposite angles are equal.
Q8: What is the difference between a square and a rhombus?
A8: A square is a type of rhombus with all four sides equal and all angles equal to 90 degrees. However, a rhombus may have all sides equal but not necessarily all angles equal to 90 degrees.
Q9: What do you mean by convex polygon?
A9: Polygons that have any line segment joining any two different points in the interior and have no portions of their diagonals in their exteriors are called convex polygons.
Q10: What do you mean by concave polygon?
A10: Polygons that have one diagonal outside it are called concave polygons.
Q11: What do you mean by regular polygon?
A11: A polygon whose all sides, all angles are equal that is which is both equiangular and equilateral are called regular polygon.
Example: Square; Equilateral triangle
Q12: What do you mean by irregular polygon?
A12: Polygon whose all sides are not equal are called Irregular polygon.
Example: Rectangle.
Q13: Are there any online resources or tools available for practicing understanding quadrilaterals case study questions?
A13: We provide case study questions for CBSE Class 8 Maths on our website. Students can visit the website and practice sufficient case study questions and prepare for their exams. If you need more case study questions, then you can visit Physics Gurukul website. they are having a large collection of case study questions for all classes.
Q14: What are the important points to note for CBSE Class 8 Maths Understanding Quadrilaterals?
A14: Here are some important points to observe/note
(i) Every parallelogram is a trapezium, but every trapezium is not a parallelogram.
(ii) Every rectangle, rhombus and square are parallelograms, but every parallelogram is not a rectangle or a rhombus or a square.
(iii) Every square is a rectangle, but every rectangle is not a square.
(iv) Every square is a rhombus, but every rhombus is not a square



