Lines and Angles Class 9 Assertion Reason Questions Maths Chapter 6

Q: Q4: What strategies should students use to answer assertion reason questions effectively?

A4: Students can use the following strategies: Understand Each Statement Separately: Determine if each statement is true or false independently. Analyze the Relationship: If both statements are true, check if the reason correctly explains the assertion.

Q: Q6: What are the different types of angles?

A6: Angles are classified based on their measures: Acute Angle : Measures less than 90°. Right Angle : Measures exactly 90°. Obtuse Angle : Measures more than 90° but less than 180°. Straight Angle : Measures exactly 180°. Reflex Angle : Measures more than 180° but less than 360°.

Q: Q8: What are complementary and supplementary angles?

A8: Complementary Angles : Two angles are complementary if their sum is 90°. Supplementary Angles : Two angles are supplementary if their sum is 180°.

Download CBSE and ICSE Books in PDF Format

Reading Time: 10 minutes

Last Updated on November 15, 2024 by XAM CONTENT

Hello students, we are providing case study questions for class 9 maths. Assertion Reason questions are the new question format that is introduced in CBSE board. The resources for assertion reason questions are very less. So, to help students we have created chapterwise assertion reason questions for class 9 maths. In this article, you will find assertion reason questions for CBSE Class 9 Maths Chapter 6 Lines and Angles. It is a part of Assertion Reason Questions for CBSE Class 9 Maths Series.

Chapter	Lines and Angles
Type of Questions	Assertion Reason Questions
Nature of Questions	Competency Based Questions
Board	CBSE
Class	9
Subject	Maths
Useful for	Class 9 Studying Students
Answers provided	Yes
Difficulty level	Mentioned
Important Link	Class 9 Maths Chapterwise Assertion Reason

Customised Study Materials for Teachers, Schools and Coaching Institute

Table of Contents

Assertion Reason Questions on Lines and Angles

Directions:

a. Both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).
b. Both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).
c. Assertion (A) is true but Reason (R) is false.
d. Assertion (A) is false but Reason (R) is true.

Questions:

Q. 1. Assertion (A): If angles ‘x’ and ‘y’ form a linear pair of angles and x = 70°, then y = 110°.
Reason (R): Sum of linear pair of angles is always 180°.

Q. 2. Assertion (A): The pair of angles 102°, 78° is supplementary.
Reason (R): The sum of two angles is 180°, then it is supplementary.

Q. 3. Assertion (A): In the adjoining figure, if AB || CD and ∠E = 50°, then ∠BEC is 50°.

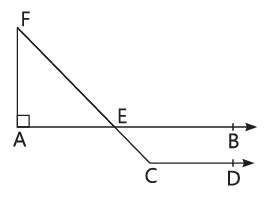
Lines and Angles Class 9 Assertion Reason Questions Maths Chapter 6 - 1

Reason (R): If sum of two angles is 90°, then it is complementary.

Also read: Lines and Angles Class 9 Case Study Questions

Solutions:

1. (a) Assertion (A): Given, x = 70°
Therefore, x + y = 180° ⇒ 70° + y = 180°
⇒ y = 110°
So, Assertion (A) is true.
Reason (R): It is true to say that the sum of linear pair of angles is 180°.
Hence, both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).

2. (a) Assertion (A): Here 102° + 78° = 180°.
Hence, pair of angles is supplementary.
So, Assertion (A) is true.

Reason (R): It is true to say that the sum of two angles is 180°, then it is supplementary.
Hence, both Assertion (A) and Reason (R) are true and Reason (R) is the correct explanation of Assertion (A).

3. (b) Assertion (A): Given, ∠FEA = 50°, ∠BEC = ∠FEA = 50° (Vertically opposite angles)
So, Assertion (A) is true.
Reason (R): It is also true to say that in complementary angles, their sum is 90°.
Hence, both Assertion (A) and Reason (R) are true but Reason (R) is not the correct explanation of Assertion (A).

Understanding Lines and Angles

Line: A geometrical object that is straight and extends indefinitely in both directions.
Line Segment: A part of a line with two end points.
Ray: A part of line with one end point.
Collinear Points: Three or more points lying on the same line are known as collinear points. Otherwise, they are non-collinear points.
Angle: It is formed when two rays originate from the same end point. The rays are called arms and the end point is called vertex.

Types of Angles:

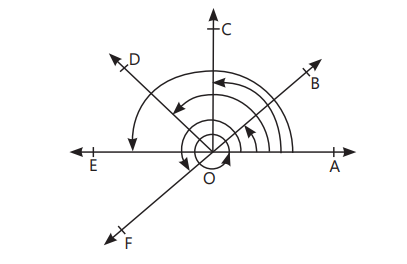
Acute Angle: An angle with measure more than 0° but less than 90°. In figure, ∠AOB is acute angle.
Obtuse Angle: An angle with measure more than 90° but less than 180°. In figure, ∠AOD is obtuse angle.
Right Angle: An angle with measure exactly 90°. In figure, ∠AOC is right angle.
Straight Angle: An angle with measure 180°. In figure, ∠AOE is straight angle.
Reflex Angle: An angle with measure more than 180° but less than 360°. In figure, ∠AOF is reflex angle, when measured anticlockwise.
Complete Angle: An angle with measure 360°. In figure, ∠AOA is complete angle.

Pair of Angles:

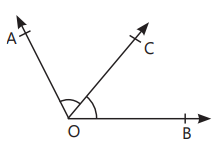
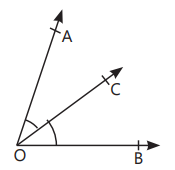
Complementary Angles: Two angles with the sum of 90°. In above figure, ∠AOB + ∠BOC = 90°, so ∠AOB and ∠BOC are complementary angles.
Supplementary Angles: Two angles with the sum of 180°. In above figure, ∠AOB + ∠BOE = 180°, so ∠AOB and ∠BOE are supplementary angles
Adjacent Angles: Two angles having a common vertex and a common arm with uncommon arms on either side of the common arm. In figure, ∠AOC and ∠BOC are adjacent angles. OR When two angles are adjacent, then their sum is always equal to the angle formed by the two non-common arms. In figure, ∠AOB = ∠AOC + ∠BOC
Linear Pair of Angles: Two adjacent angles with the sum of 180°. In figure, ∠AOC and ∠BOC are linear pair of angles.

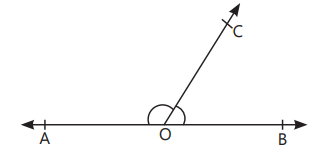
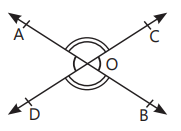
Vertically Opposite Angles: The pair of angles lying on the opposite sides of the point of intersection. In figure, (∠AOC and ∠BOD) and
(∠AOD and ∠BOC) are pairs of vertically opposite angles.

Bisector of an Angle: A ray which divides an angle into two equal parts.

Also check

Topics from which assertion reason questions may be asked

Basic Terms and Definitions
Types of Angles
Intersecting Lines and Non-Intersecting Lines
Pairs of Angles
Parallel Lines and a Transversal
Angle Sum Property of a Triangle

The length of perpendiculars at different points on the parallel lines is same.

Assertion reason questions from the above given topic may be asked.

Helpful Links for CBSE Class 9 Preparation

Download Customised White Label Study Materials in MS Word Format

We are providing teaching resources to teachers and coaching institute looking for customised study materials in MS word format. Our High-quality editable study material which is prepared by the expert faculties are Highly useful for Teachers, Mentors, Tutors, Faculties, Coaching Institutes, Coaching Experts, Tuition Centers.

Download Product Brochure

Frequently Asked Questions (FAQs) on Lines and Angles Assertion Reason Questions Class 9

Q1: What are assertion reason questions?

A1: Assertion-reason questions consist of two statements: an assertion (A) and a reason (R). The task is to determine the correctness of both statements and the relationship between them. The options usually include:
(i) Both A and R are true, and R is the correct explanation of A.
(ii) Both A and R are true, but R is not the correct explanation of A.
(iii) A is true, but R is false.
(iv) A is false, but R is true. or A is false, and R is also false.

Q2: Why are assertion reason questions important in Maths?

A2: Students need to evaluate the logical relationship between the assertion and the reason. This practice strengthens their logical reasoning skills, which are essential in mathematics and other areas of study.

Q3: How can practicing assertion reason questions help students?

A3: Practicing assertion-reason questions can help students in several ways:
Improved Conceptual Understanding: It helps students to better understand the concepts by linking assertions with their reasons.
Enhanced Analytical Skills: It enhances analytical skills as students need to critically analyze the statements and their relationships.
Better Exam Preparation: These questions are asked in exams and practicing them can improve your performance.

Q4: What strategies should students use to answer assertion reason questions effectively?

A4: Students can use the following strategies:
Understand Each Statement Separately: Determine if each statement is true or false independently.
Analyze the Relationship: If both statements are true, check if the reason correctly explains the assertion.

Q5: What are common mistakes to avoid when answering Assertion Reason questions?

A5: Common mistakes include:
Not reading the statements carefully and missing key details.
Assuming the Reason explains the Assertion without checking the logical connection.
Confusing the order or relationship between the statements.
Overthinking and adding information not provided in the question.

Q6: What are the different types of angles?

A6: Angles are classified based on their measures:
Acute Angle: Measures less than 90°.
Right Angle: Measures exactly 90°.
Obtuse Angle: Measures more than 90° but less than 180°.
Straight Angle: Measures exactly 180°.
Reflex Angle: Measures more than 180° but less than 360°.

Q7: What is the Angle Sum Property of a Triangle?

A7: The Angle Sum Property states that the sum of the interior angles of a triangle is always 180°.

Q8: What are complementary and supplementary angles?

A8: Complementary Angles: Two angles are complementary if their sum is 90°.
Supplementary Angles: Two angles are supplementary if their sum is 180°.

Q9: What is a linear pair of angles?

A9: A linear pair of angles is formed when two adjacent angles add up to 180°. The angles in a linear pair are always supplementary.

Q10: Are there any online resources or tools available for practicing Lines and Angles assertion reason questions?

A10: We provide assertion reason questions for CBSE Class 9 Maths on our website. Students can visit the website and practice sufficient assertion reason questions and prepare for their exams. If you need more assertion reason questions, then you can visit Physics Gurukul website. they are having a large collection of assertion reason questions for all classes.