Last Updated on December 24, 2024 by XAM CONTENT
Hello students, here you will find numerical on average speed and average velocity with answers. Before we start solving the numerical, let’s see some important points and formulae. This will help you to solve the problems efficiently.
| Topic | Average Speed and Average Velocity |
| Type of Questions | Numerical Problems |
| Nature of Questions | Formula Based |
| Board | CBSE |
| Class | 9 |
| Subject | Science – Physics |
| Useful for | Class 9 Studying Students |
| Answers provided | Yes |
| Difficulty level | Mentioned |
| FAQ | Provided |
| Important Link | Class 9 Physics Topicwise Numerical Problems |
Understanding Average Speed and Average Velocity
Understanding the concepts of average speed and average velocity is fundamental in the study of motion in physics. While they may seem similar at first glance, they describe different aspects of motion and are calculated differently.
Average Speed:
Average speed is a scalar quantity that represents the total distance traveled divided by the total time taken. It does not take into account the direction of travel, only the magnitude of the distance covered.
Average speed = Total distance/Total time
To calculate average speed, you sum up all the distances traveled and divide by the total time. For example, if a car travels 100 km north in 2 hours, then 50 km south in 1 hour, the average speed is:
Total Distance = 100km + 50km = 150km
Total Time = 2 hours + 1 hour = 3 hours
Therefore, Average speed = 150/3 = 50 km/hour
Average Velocity:
Average velocity, on the other hand, is a vector quantity that represents the total displacement (change in position) divided by the total time taken. Displacement considers the direction from the starting point to the final position.
Average speed = Total displacement/Total time
To calculate average velocity, you need the total displacement, which is the straight-line distance from the starting point to the final position, considering direction. Using the same example:
Total Displacement = 100 km north − 50 km south = 50 km north
Total Time=3 hours
Therefore, Average velocity = 50/3 = 16.67 km/hour north
Average speed is a scalar quantity whereas average velocity is a vector quantity.
In the below section, we are providing numerical problems on Average Speed and Average Velocity for Class 9 Physics.
Numerical Problems on Average Speed and Average Velocity with Answers
Formula used:
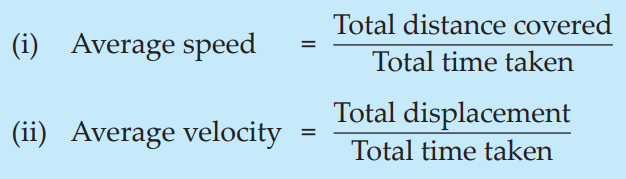
Units used:
SI unit of average speed and average velocity is m/s or ms-1.
Numerical Problem 1:
An athlete is running on a circular track. He runs a distance of 400 m in 25 s before returning to his original position. What is his average speed and velocity?
Difficulty Level: Medium
Ans. The athlete runs at an average speed of 16 m/s and velocity 0 m/s.
Numerical Problem 2:
A person swims 100 m in the first 40 s, 80 m in the next 40 s and 45 m in the last 20 s. What is the average speed?
Difficulty Level: Easy
Ans. The person swims with an average speed of 2.25 m/s.
Numerical Problem 3:
An object moves 18 m in the first 3 sec, 22 m in the next 3 sec and 14 m in the last 3 sec. What is its average speed?
Difficulty Level: Easy
Ans. The object moves with an average speed of 6 m/s.
Numerical Problem 4:
A person travels a distance of 72 km in 4 hours. Calculate average speed in m/s.
Difficulty Level: Easy
Ans. The person travels with average speed of 5 m/s
Numerical Problem 5:
A person runs 100 m in the first 50 s. 80 m in the next 30 s and 45 m in the last 35 s. What is the average speed?
Difficulty Level: Easy
Ans. 1.95 m/s
Numerical Problem 6:
An object moves 26 m in first 3 seconds and 16 m in the next 3 seconds while it travels 18 m in the last 3 seconds. Calculate average speed.
Difficulty Level: Easy
Ans. 6.67 m/s
Helpful Links for CBSE Class 9 Science Preparation
- Download Latest Sample Papers for CBSE Class 9 Science
- Download Worksheets for CBSE Class 9 Science
- Download Chapter Tests for CBSE Class 9 Science
- Download Case Study Question Bank for CBSE Class 9 Science
- Download Numerical Problems for CBSE Class 9 Physics
- Download Important MCQs for CBSE Class 9 Physics
Frequently Asked Questions (FAQs) on Average Speed and Average Velocity Numerical Problems
Q1: Why is it important to solve numerical problems on average speed and average velocity?
A1: Solving numerical problems on average speed and average velocity is crucial for several reasons:
Conceptual Understanding: It helps solidify theoretical concepts by applying them to practical scenarios.
Problem-Solving Skills: It enhances analytical and problem-solving skills, which are vital in physics and other scientific disciplines.
Application of Formulas: It provides practice in using and manipulating formulas, which is essential for mastering physics.
Preparation for Advanced Topics: It builds a strong foundation for more complex topics in kinematics and dynamics.
Q2: How do numerical problems prepare students for exams?
A2: Numerical problems prepare students for exams in several ways:
Practice and Familiarity: Regular practice with numerical problems makes students familiar with the types of questions they may encounter in exams.
Time Management: Solving numerical problems helps students develop the ability to manage their time effectively during exams.
Confidence Building: Successfully solving numerical problems boosts confidence, reducing exam anxiety.
Error Identification: It helps students identify common mistakes and learn from them, improving accuracy in exams.
Q3: Why are numerical problems useful for understanding physics?
A3: Numerical problems are useful for understanding physics because:
Practical Application: They allow students to apply theoretical knowledge to practical situations, enhancing understanding.
Critical Thinking: They encourage critical thinking and logical reasoning, essential for comprehending physical phenomena.
Interconnected Concepts: They demonstrate how different concepts in physics are interconnected, providing a holistic understanding.
Visualization: They often involve diagrams and visual aids, helping students visualize and grasp abstract concepts better.
Q4: What are the key steps to solve numerical problems on average speed and average velocity?
A4: The key steps to solve numerical problems on average speed and average velocity are:
Read the Problem Carefully: Understand the given data and what is being asked.
Identify the Known and Unknown Variables: List out the known quantities and what needs to be calculated.
Select the Appropriate Formula: Choose the correct formula based on the known and unknown variables.
Perform the Calculations: Substitute the known values into the formula and solve for the unknown.
Check the Units: Ensure the units are consistent and convert them if necessary.
Review the Answer: Check if the answer is reasonable and verify it with the context of the problem.
Q5: What tips can help students improve their skills in solving numerical problems?
A5: Here are some tips to improve skills in solving numerical problems:
Practice Regularly: Consistent practice is key to mastering numerical problems.
Understand the Concepts: Ensure a strong grasp of the underlying concepts before attempting problems.
Review Mistakes: Learn from errors by reviewing and understanding where you went wrong.
Q6: Are there any online resources for practicing numerical problems on average speed and average velocity?
A6: Yes, there are several online resources available for practicing numerical problems, including:
Educational Websites: Websites like Physics Gurukul offer practice problems and tutorials.
xamcontent.com: Xam Content also offers numerical problems on different topics for all classes.
Q7: What are the differences between average speed and average velocity?
A7: Differences between average speed and average velocity are given below-
Nature: Average speed is a scalar quantity (only magnitude), while average velocity is a vector quantity (magnitude and direction).
Calculation: Average speed is the total distance divided by total time, whereas average velocity is the total displacement divided by total time.
Path Dependence: Average speed considers the entire path traveled, while average velocity considers only the straight-line distance between the starting and ending points.
Units: Both average speed and average velocity are measured in units of distance per time (e.g., km/h, m/s), but velocity includes direction.




