Last Updated on October 26, 2024 by XAM CONTENT
Hello students, we are providing maths formulas for class 10 maths. In CBSE Class 10, mastering maths formulas is crucial for solving problems efficiently in board exams. Knowing these formulas allows students to tackle a wide range of problems without hesitation, saving time and increasing accuracy.
Formula List for Class 10 Maths Board Exams
Maths Formulas for Class 10 CBSE Chapter 2 Polynomials
Relationship between Zeroes and Coefficients of a Polynomial
(i) Zero of a linear polynomial $a x+b$ is $x=-\frac{b}{a}$
(ii) If $\alpha$ and $\beta$ are the zeroes of the quadratic polynomial $a x^2+b x+c$, then $\alpha+\beta=-\frac{b}{a}$
i.e. sum of zeroes $=-\frac{\text { Coefficient of } x}{\text { Coefficient of } x^2}$
and $\alpha \beta=\frac{c}{a}$
i.e. product of zeroes $=\frac{\text { Constant term }}{\text { Coefficient of } x^2}$
(iii) If $\alpha, \beta$ and $\gamma$ are zeroes of the cubic polynomial then $\alpha+\beta+\gamma=-\frac{b}{a}$
i.e. sum of zeroes $=-\frac{\text { Coefficient of } x^2}{\text { Coefficient of } x^3}$
$\alpha \beta+\beta \gamma+\gamma \alpha=\frac{c}{a}$
i.e. sum of product of every two root $=\frac{\text { Coefficient of } x}{\text { Coefficient of } x^3}$
and $\alpha \beta \gamma=-\frac{d}{a}$
i.e. product of roots $=-\frac{\text { Constant term }}{\text { Coefficient of } x^3}$
Maths Formulas for Class 10 CBSE Chapter 3 Pair of Linear Equations in Two Variables
Consistency and Nature of the Graphs
Consider the standard form of linear equations in two variables.
Maths Formulas for Class 10 CBSE Chapter 4 Quadratic Equations
Quadratic Formula
Consider a quadratic equation: $\mathrm{ax}^2+\mathrm{bx}+\mathrm{c}=0$.
If $b^2-4 a c \geq 0$, then the roots of the above equation are given by:
$$
x=\frac{-b \pm \sqrt{b^2-4 a c}}{2 a}
$$
Nature of Roots
For quadratic equation $a x^2+b x+c=0$
$(a \neq 0)$, value of $\left(b^2-4 a c\right)$ is called discriminant of the equation and denoted as D .
$$
\therefore D=b^2-4 a c
$$
Discriminant is very important in finding nature of the roots.
(i) IfD $=0$, then roots are real and equal.
(ii) If $D>0$, then roots are real and unequal
(iii) If $D<0$, then roots are not real.
Maths Formulas for Class 10 CBSE Chapter 5 Arithmetic Progressions
$\mathbf{n}^{\text {th }}$ Term (or General Term) of an Arithmetic Progressions
In an AP, with first term ‘ $a$ ‘ and common difference $d$, the $n^{\text {th }}$ temr (or the general term) is given by,
$$
a_n=a+(n-1) d
$$
Note: An AP can be finite or infinite according to as the number of terms are finite or infinite.
If there are m terms in an AP, then $\mathrm{a}_{\mathrm{m}}$ is the last term $\&$ is sometimes denoted by ‘$l$’.
Sum of the FIRST ‘$n$’ Terms of an A.P.
(i) The sum of the first n terms of an A.P. is given by
$$
S_n=\frac{n}{2}[2 a+(n-1) d]
$$
where a is the first term and d is the common difference.
(ii) If $l$ is the last term of the finite A.P. say the $n^{\text {th }}$ term, then the sum of all terms of the A.P. is given by,
$$
S_n=\frac{n}{2}[a+l]
$$
Note: Sum of first $n$ positive integers is given by
$$
S_n=\frac{n(n+1)}{2}
$$
Maths Formulas for Class 10 CBSE Chapter 6 Triangles
Criteria for Similarity of Triangles
(i) AAA Similarity Criterion: If in two triangles, corresponding angles are equal, then their corresponding sides are in the same ratio and hence the two triangles are similar.
(ii) AA Similarity Criterion: If in two triangles, two angles of one triangle are respectively equal to the two angles of the other triangle, then the two triangles are similar.
(iii) SSS Similarity Criterion: If in two triangles, corresponding sides are in the same ratio then their correspoding angles are equal and hence the triangles are similar.
(iv) SAS Similarity Criterion: If one angle of a triangle is equal to one angle of another triangle and the sides including these angles are in the same ratio (proportion), then the two triangles are similar.
Maths Formulas for Class 10 CBSE Chapter 7 Coordinate Geometry
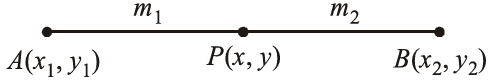
Distance Formula
The distance between any two points $\mathrm{P}\left(\mathrm{x}_1, \mathrm{y}_1\right)$ and $\mathrm{Q}\left(\mathrm{x}_2, \mathrm{y}_2\right)$ in the plane is given by,
$$
P Q=\sqrt{\left(x_1-x_2\right)^2+\left(y_1-y_2\right)^2}
$$
Also the distance of the point $\mathrm{P}\left(\mathrm{x}_1, \mathrm{y}_1\right)$ from the origin is
$$
\sqrt{x_1^2+y_1^2}
$$
Section Formula
The coordinates of the point $P(x, y)$ which divides the line segment joining the points $A\left(x_1, \mathrm{y}_1\right)$ and $\mathrm{B}\left(x_2, y_2\right)$ internally in the ratio $\mathrm{m}_1: \mathrm{m}_2$
i.e., PA/PB = m1/m2
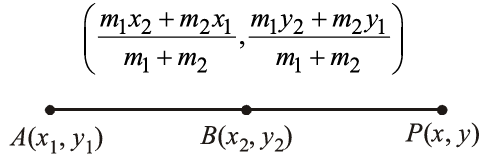
(ii) The coordinates of the point $P(x, y)$ which divides the line segment joining the points $A\left(x_1, y_1\right)$ and $B\left(x_2, y_2\right)$ externally in the ratio, $\mathrm{m}_1: \mathrm{m}_2$ i.e., $\frac{P A}{P B}=\frac{m_1}{m_2}$ are
$$
\left(\frac{m_1 x_2-m_2 x_1}{m_1-m_2}, \frac{m_1 y_2-m_2 y_1}{m_1-m_2}\right)
$$
(iii) If the ratio in which $P$ divides $A B$ is $K: 1$, then the coordinates of the point $P$ will be
$$
\left(\frac{K x_2+x_1}{K+1}, \frac{K y_2+y_1}{K+1}\right)
$$
Mid-point Formula
The coordinates of the mid point $P$ of the line segment joining the points $A\left(x_1, \mathrm{y}_1\right)$ and $B\left(x_2, y_2\right)$ is
$$
\left(\frac{x_1+x_2}{2}, \frac{y_1+y_2}{2}\right)
$$
Area of a Triangle
The area of $\triangle \mathrm{ABC}$ formed by the vertices $A\left(x_1, y_1\right), B\left(x_2, y_2\right)$ and $C\left(x_3, y_3\right)$ is given by
$$
\frac{1}{2}\left|x_1\left(y_2-y_3\right)+x_2\left(y_3-y_1\right)+x_3\left(y_1-y_2\right)\right|
$$
Note:
(i) Area of triangle $=\frac{1}{2} \times$ base $\times$ Altitude
(ii) Area of polygon can be calculated by dividing it into the triangular region.
(iii) If theree points are collinear then area of the triangle formed by them is zero.
Maths Formulas for Class 10 CBSE Chapter 8 Introduction to trigonometry
Trigonometric Ratios
(i) sinA = P/H (ii) cosA = B/H (iii) tanA = P/B
(iv) sinA. cosecA = 1 (v) cosA. secA = 1 (vi) tanA. cotA = 1
(vii) cosecA = H/P (viii) secA = H/B (ix) cotA = B/P
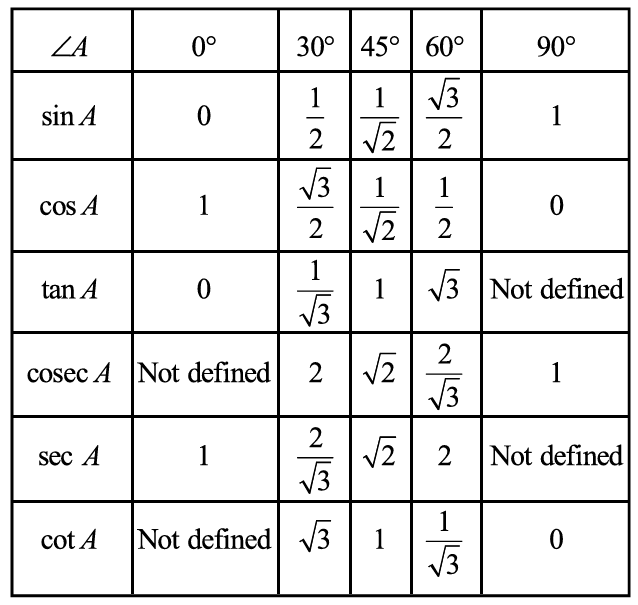
Trigonometric Ratios of Some Specific Angles
Trigonometric Ratios of Complementary Angles:
We have following relationship for complementary angles:
$$
\begin{aligned}
& \sin \left(90^{\circ}-\theta\right)=\cos \theta, \cos \left(90^{\circ}-\theta\right)=\sin \theta \\
& \tan \left(90^{\circ}-\theta\right)=\cot \theta, \cot \left(90^{\circ}-\theta\right)=\tan \theta \\
& \sec \left(90^{\circ}-\theta\right)=\operatorname{cosec} \theta, \operatorname{cosec}\left(90^{\circ}-\theta\right)=\sec \theta
\end{aligned}
$$
$$
\text { for all values of } \theta \text { lying between } 0^{\circ} \text { and } 90^{\circ} \text {.}
$$
Note : Here $(90-\mathrm{A})^{\circ}$ is the complementary angle of A.
Trigonometric Identities
An equation involving trigonometric ratios of an angle is called a trigonometric identity, if it is true for all values of the angle(s) involved.
(i) $\sin ^2 \theta+\cos ^2 \theta=1$
(ii) $\sec ^2 \theta-\tan ^2 \theta=1$
(iii) $\operatorname{cosec}^2 \theta-\cot ^2 \theta=1$
Maths Formulas for Class 10 CBSE Chapter 10 Circles
Theorem Related to Length of Tangents
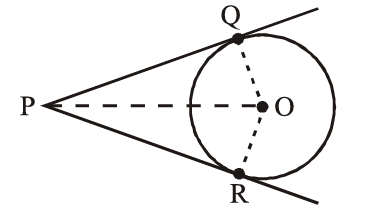
(i) From the External Points The lengths of tangents drawn from an external point to a circle are equal. i.e.,
Here, PQ and QR are the two tangents drawn from P to the circle. Here OP is the angle bisector of ∠QPR, i.e., the centre lies on the bisector of the angle between the two tangents.
Maths Formulas for Class 10 CBSE Chapter 12 Areas Related to Circles
Circumference and Area of a Circle
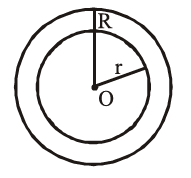
(i) The perimeter or circumference of a circle is defined as distance covered by travelling once around a circle and is given by $\mathrm{C}=2 \pi \mathrm{r}=\pi \mathrm{d}$
where $r=$ radius of the circle and
$\mathrm{d}=$ diameter of the circle.
(ii) The area of a circle of radius r is given by, $\mathrm{A}=\pi r^2=\frac{\pi}{4} d^2$ where, $d=$ diameter of the circle.
(iii) Area of a circular ring: The area of the circular path or ring is given by the difference of the area of outer circle and the area of inner circle. Area of circular ring $=\pi\left(R^2-r^2\right)$
Length of an Arc and Area of Sector
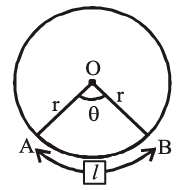
(i) The length of an arc of a sector of an angle $\theta$ is given by,
$$
l=\frac{\theta}{360} \times 2 \pi r
$$
Perimeter of sector $A O B=O A+O B+\overparen{A B}=2 r+\frac{\theta}{360} \times 2 \pi r$
(ii) The area of the sector AOB of angle $\theta=\frac{\theta}{360^{\circ}} \times \pi r^2$
This is the area of minor sector.
$\therefore \quad$ area of major sector $\mathrm{AOB}=\pi \mathrm{r}^2-$ Area of minor sector AOB
Area of a Segment
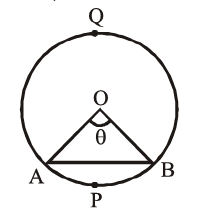
(i) Area of segment $\mathrm{APB}=\mathrm{Area}($ sector OAPB$)-\operatorname{Area}(\triangle \mathrm{OAB})$ $=\frac{\theta}{360} \times \pi r^2-$ area of $\triangle O A B$
This is the area of minor segment.
$\therefore \quad$ area of major segment $A Q B$ $=\pi r^2-$ Area of minor segment APB
(ii) If $\theta$ is the central angle, then the area of segment APB $=\frac{\theta}{360} \times \pi r^2-r^2 \sin \frac{\theta}{2} \cos \frac{\theta}{2}$
Maths Formulas for Class 10 CBSE Chapter 13 Surface Areas and Volumes
Cone
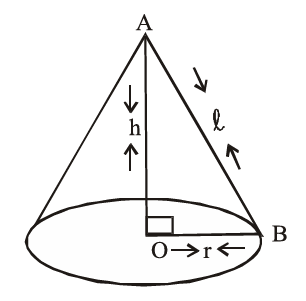
(i) Volume of cone $=\frac{1}{3} \pi r^2 h$
(ii) C.S.A or L. S. A $=\pi r \ell$ where slant height
$$
=\ell=\sqrt{\mathrm{r}^2+\mathrm{h}^2}
$$
(iii) T. S. A of cone $=\pi \mathrm{r} \ell+\pi \mathrm{r}^2$
Sphere and Hemi-sphere
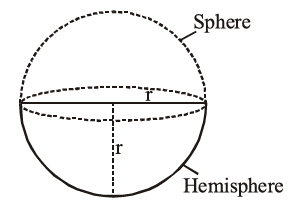
(i) Surface area of sphere $=4 \pi \mathrm{r}^2$
(ii) Volume of a sphere $=\frac{4}{3} \pi \mathrm{r}^3$
(iii) Volume of hemisphere $=\frac{2}{3} \pi \mathrm{r}^3$
(iv) C.S.A. of hemisphere $=2 \pi \mathrm{r}^2$
(v) Total surface area of Hemi-sphere $=2 \pi \mathrm{r}^2+\pi \mathrm{r}^2=3 \pi \mathrm{r}^2$
Spherical shell/Hemi-spherical shell
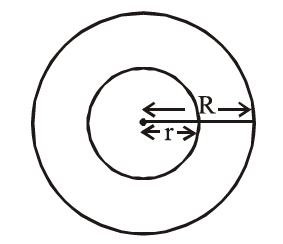
(i) Outer surface area of spherical shell $=4 \pi \mathrm{R}^2$
(ii) Inner S.A. of spherical shell $=4 \pi \mathrm{r}^2$
(iii) Total surface area of spherical shell $=4 \pi\left(\mathrm{R}^2+\mathrm{r}^2\right)$
(iv) Volume of spherical shell of external radius R and internal radius ‘ $r$ ‘ $=\frac{4}{3} \pi\left(R^3-r^3\right)$
(v) Outer curved surface area of hemispherical shell $=2 \pi R^2$
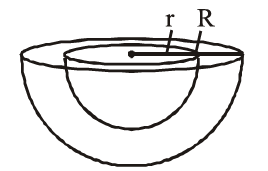
(vi) Inner curved surface area of hemispherical shell $=2 \pi \mathrm{r}^2$
(vii) Thick hemispherical bowl of external and internal radii R and r , Total S.A. $=\pi\left(3 \mathrm{R}^2+\mathrm{r}^2\right)$
(viii) Volume of hemispherical shell of external radius ‘ $R$ ‘ and internal radius ‘ $r$ ‘ $=\frac{2}{3} \pi\left(\mathrm{R}^3-\mathrm{r}^3\right)$.
Why Memorizing Formulas is Essential for Class 10 Maths
Memorizing maths formulas equips students with the tools needed to solve complex questions during exams. Here are some reasons why formulas are indispensable:
- Efficiency: With formulas at their fingertips, students can apply them directly to solve questions without additional calculations.
- Foundation Building: Formulas form the basis for advanced mathematics, making it easier to understand more complex concepts in higher classes.
- Quick Revision: Memorized formulas allow students to revise quickly, especially helpful in high-pressure exam situations.
How to Effectively Memorize Maths Formulas for Class 10
For many students, memorizing formulas can be challenging, but certain strategies can make the process easier:
- Practice Regularly: Practicing problems with specific formulas helps reinforce their usage and structure.
- Break Down Complex Formulas: Simplify large formulas by dividing them into smaller parts and understanding each part’s significance.
- Group Formulas by Topic: Grouping related formulas together makes it easier to learn and apply them.
Tips for Using Class 10 Maths Formulas Effectively in Exams
Using formulas correctly during exams can maximize scores:
- Identify the Formula First: Before diving into a solution, determine which formula applies to avoid calculation errors.
- Check Units: For questions involving measurements, ensure that units are consistent when applying formulas.
- Verify Answers: After solving, plug values back into the formula to verify accuracy where possible.
- Avoid Formula Cramming at the Last Minute: Regular review helps retain formulas better than last-minute cramming.
Mastering maths formulas for CBSE Class 10 not only aids in scoring better in board exams but also builds a foundation for higher studies. With consistent practice, effective memorization techniques, and understanding each formula’s application, students can approach exams with confidence and precision.
Frequently Asked Questions (FAQ) on Maths Formulas for Class 10
Q1: Why is it important to memorize all Maths formulas for CBSE Class 10?
A1: Memorizing formulas allows students to solve questions faster and more accurately in exams. A solid understanding helps in confidently approaching various types of questions, saving time and reducing errors.
Q2: What are the best strategies to remember Maths formulas for Class 10?
A2: Using grouping formulas by chapter, and regular practice are effective ways. Writing down formulas repeatedly also improves retention and familiarity.
Q3: Which chapters in Class 10 Maths have the most formulas to remember?
A3: Chapters like Trigonometry, Surface Areas and Volumes, and Quadratic Equations have essential formulas that frequently appear in exams, making them high-priority for students.
Q4: How can I effectively revise Class 10 Maths formulas before exams?
A4: Set aside time each day to review formulas and solve a few problems from each chapter. Using a summary chart or formula sheet can provide a quick overview before exams.
Q5: Are all Maths formulas in Class 10 provided in the NCERT textbook?
A5: Yes, the NCERT Class 10 Maths textbook covers essential formulas. Additional resources, like study guides or class notes, can be helpful for extended understanding and applications.
Q6: How much of the Class 10 Maths exam relies on formulas?
A6: A significant portion involves formula-based questions, especially in topics like Trigonometry, Algebra, and Mensuration. Knowing formulas well is essential for solving problems quickly and accurately.
Q7: Can practicing formulas improve my problem-solving speed?
A7: Absolutely! Familiarity with formulas saves time during exams, as students can apply them directly instead of deriving them from scratch, improving overall problem-solving speed.



