Triangles Class 10 Case Study Questions Maths Chapter 6

Reading Time: 8 minutes

Last Updated on September 4, 2025 by XAM CONTENT

Hello students, we are providing case study questions for class 10 maths. Case study questions are the new question format that is introduced in CBSE board. The resources for case study questions are very less. So, to help students we have created chapterwise case study questions for class 10 maths. In this article, you will find case study questions for CBSE Class 10 Maths Chapter 6 Triangles. It is a part of Case Study Questions for CBSE Class 10 Maths Series.

Chapter	Triangles
Type of Questions	Case Study Questions
Nature of Questions	Competency Based Questions
Board	CBSE
Class	10
Subject	Maths
Unit	Unit 4 Geometry
Useful for	Class 10 Studying Students
Answers provided	Yes
Difficulty level	Mentioned
Important Link	Class 10 Maths Chapterwise Case Study

Case Study Questions on Triangles

Questions

Passage 1:

Anika is studying in class X. She observe two poles DC and BA. The heights of these poles are x m and y m respectively as shown in figure:

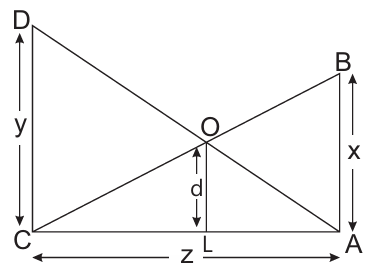
These poles are z m apart and O is the point of intersection of the lines joining the top of each pole to the foot of opposite pole and the distance between point O and L is d. Few questions came to his mind while observing the poles.

Based on the above information, solve the following questions:

Q. 1. Which similarity criteria is applicable in ΔCAB and ΔCLO?

Q. 2. If CL = a, then find a in terms of x, y and d.

Q. 3. If AL = b, then find b in terms of x, y and d.

Answers

1. In ΔCAB and ΔCLO, we have
∠CAB = ∠CLO = 90°
∠C = ∠C (common)
By AA similarity criterion,
ΔCAB ~ ΔCLO

2. ΔCAB ~ ΔCLO

$$
\therefore \quad \frac{\mathrm{CA}}{\mathrm{CL}}=\frac{\mathrm{AB}}{\mathrm{LO}} \Rightarrow \frac{z}{a}=\frac{x}{d} \Rightarrow a=\frac{z d}{x}
$$

3. In $\triangle A L O$ and $\triangle A C D$,

We have

$$
\begin{gathered}
\angle \mathrm{ALO}=\angle \mathrm{ACD}=90^{\circ} \\
\angle \mathrm{A}=\angle \mathrm{A}
\end{gathered}
$$

$\therefore$ By AA similarity criterion,

$$
\triangle \mathrm{ALO} \sim \triangle \mathrm{ACD}
$$

$$
\begin{aligned}
\therefore \frac{A L}{A C}=\frac{O L}{D C} & \Rightarrow \frac{b}{z}=\frac{d}{y} \\
& \Rightarrow b=\frac{z d}{y}
\end{aligned}
$$

Also check

• Introduction to Trigonometry Class 10 Case Study Questions Maths Chapter 8
• Coordinate Geometry Class 10 Case Study Questions Maths Chapter 7
• Triangles Class 10 Case Study Questions Maths Chapter 6
• Arithmetic Progressions Class 10 Case Study Questions Maths Chapter 5
• Quadratic Equations Class 10 Case Study Questions Maths Chapter 4
• Pair of Linear Equations in Two Variables Class 10 Case Study Questions Maths Chapter 3
• Polynomials Class 10 Case Study Questions Maths Chapter 2
• Real Numbers Class 10 Case Study Questions Maths Chapter 1

Topics from which case study questions may be asked

• Definitions, Examples, and Counter Examples of Similar Triangles
• Theorems on Similar Triangles:
  • Prove: A line parallel to one side of a triangle divides the other two sides in the same ratio.
  • Motivate: A line dividing two sides of a triangle in the same ratio is parallel to the third side.
  • Motivate: Triangles with corresponding angles equal and corresponding sides proportional are similar.
  • Motivate: Triangles with corresponding sides proportional have equal corresponding angles and are similar.
  • Motivate: Triangles with one angle equal and the sides including these angles proportional are similar.

Case study questions based on above topics may be asked.

Understanding Triangles

Similar Figures

Two figures are similar if they have the same shape (not necessarily the same size).

Similar Triangles

Two triangles are said to be similar if:

1. Their corresponding angles are equal.
2. Their corresponding sides are in the same ratio (proportional).

Basic Proportionality Theorem (BPT) / Thales’ Theorem

In a triangle, if a line is drawn parallel to one side to intersect the other two sides, then it divides those sides in the same ratio.

Converse: If a line divides two sides of a triangle in the same ratio, then it is parallel to the third side.

Criteria for Similarity of Triangles

1. AAA (or AA) Similarity: If corresponding angles of two triangles are equal, the triangles are similar.

2. SSS Similarity: If all three sides of one triangle are proportional to the three sides of another triangle, then the triangles are similar.

3. SAS Similarity: If one pair of corresponding sides is proportional and the included angle is equal, the triangles are similar.

Note: All congruent triangles are similar, but not all similar triangles are congruent.

Other Theorems

Mid-Point Theorem: The line joining the mid-points of two sides of a triangle is parallel to the third side and half of it.

Angle Bisector Theorem: The internal bisector of an angle of a triangle divides the opposite side into segments proportional to the other two sides.

Properties of Similar Triangles

If two triangles are similar:

1. Their corresponding sides, medians, and altitudes are proportional.
2. The ratio of the perimeters is equal to the ratio of their corresponding sides.
3. The ratio of the areas of two similar triangles is equal to the square of the ratio of their corresponding sides.

Similar Figures: Two figures having the same shapes (and not necessarily the same size) are called similar figures.

Frequently Asked Questions (FAQs) on Triangles Case Study