Coordinate Geometry Class 10 Case Study Questions Maths Chapter 7

Reading Time: 7 minutes

Last Updated on September 4, 2025 by XAM CONTENT

Hello students, we are providing case study questions for class 10 maths. Case study questions are the new question format that is introduced in CBSE board. The resources for case study questions are very less. So, to help students we have created chapterwise case study questions for class 10 maths. In this article, you will find case study questions for CBSE Class 10 Maths Chapter 7 Coordinate Geometry. It is a part of Case Study Questions for CBSE Class 10 Maths Series.

Chapter	Coordinate Geometry
Type of Questions	Case Study Questions
Nature of Questions	Competency Based Questions
Board	CBSE
Class	10
Subject	Maths
Unit	Unit 3 Coordinate Geometry
Useful for	Class 10 Studying Students
Answers provided	Yes
Difficulty level	Mentioned
Important Link	Class 10 Maths Chapterwise Case Study

Case Study Questions on Coordinate Geometry

Questions

Passage 1:

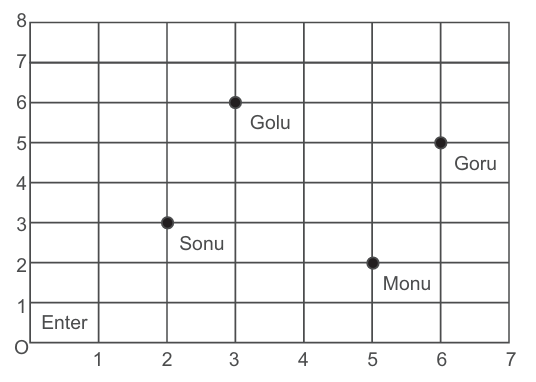
Sonu went to a lab near to his home for COVID 19 test along with his family members. The seats in the waiting area were as per the government norms of distancing during the COVID 19 pandemic (as shown in the above figure). His family members took their seats which are represented as black circular dots.

Q 1. Considering $\mathbf{O}$ as the origin, what are the coordinates of seat of Sonu and Goru respectively?
a. $(2,3)$ and $(6,5)$
b. $(3,2)$ and $(5,6)$
c. $(3,6)$ and $(5,2)$
d. $(6,3)$ and $(2,5)$

Q 2. What is the distance between Golu and Monu?
a. $\sqrt{5}$ units
b. $2 \sqrt{5}$ units
c. $3 \sqrt{5}$ units
d. $4 \sqrt{5}$ units

Q 3. What will be the coordinates of a point exactly between Sonu and Goru where a person can be seated?
a. $\left(\frac{5}{2}, \frac{9}{2}\right)$
b. $\left(\frac{11}{2}, \frac{7}{2}\right)$
C. $(4,4)$
d. $\left(\frac{9}{2}, 4\right)$

Q 4. Find the area covered by Sonu and its members, if all four seats connected with a rope.
a. $2 \sqrt{5}$ sq. units
b. $\sqrt{10}$ sq. units
c. $2 \sqrt{10}$ sq. units
d. 10 sq. units

Q 5. If the doctor divides the rope joining Sonu and Goru in the ratio $1: 2$, then the coordinates of the seat of the doctor is:
a. $\left(\frac{10}{3}, \frac{11}{3}\right)$
b. $\left(\frac{11}{3}, \frac{10}{3}\right)$
c. $(4,4)$
d. $(3,4)$

Answers

1. Option (a) is correct.

2. Option (b) is correct.

3. Option (c) is correct.

4. Option (d) is correct.

5. Option (a) is correct.

Also check

• Introduction to Trigonometry Class 10 Case Study Questions Maths Chapter 8
• Coordinate Geometry Class 10 Case Study Questions Maths Chapter 7
• Triangles Class 10 Case Study Questions Maths Chapter 6
• Arithmetic Progressions Class 10 Case Study Questions Maths Chapter 5
• Quadratic Equations Class 10 Case Study Questions Maths Chapter 4
• Pair of Linear Equations in Two Variables Class 10 Case Study Questions Maths Chapter 3
• Polynomials Class 10 Case Study Questions Maths Chapter 2
• Real Numbers Class 10 Case Study Questions Maths Chapter 1

Topics from which case study questions may be asked

• Concepts of Coordinate Geometry
• Graphs of Linear Equations
• Distance Formula
• Section Formula (Internal Division)

Case study questions based on above topics may be asked.

Understanding Coordinate Geometry

Distance Formula

The distance between two points P(x₁, y₁) and Q(x₂, y₂) in a Cartesian plane is given by:

Distance PQ = √((x₂ − x₁)² + (y₂ − y₁)²)

Section Formula

If a point P(x, y) divides the line segment joining A(x₁, y₁) and B(x₂, y₂) in the ratio m:n, then

x = (mx₂ + nx₁) / (m + n),   y = (my₂ + ny₁) / (m + n)

Special Case: If m = n, then P is the midpoint and the formula becomes:

x = (x₁ + x₂)/2,   y = (y₁ + y₂)/2

Slope of a Line (Conceptual)

The slope of a line is the tangent of the angle it makes with the positive direction of the x-axis.

For two points P(x₁, y₁) and Q(x₂, y₂), slope m is:

m = (y₂ − y₁) / (x₂ − x₁),   (x₂ ≠ x₁)

Collinearity of Points

Three points are collinear if the slope of any two pairs is equal, i.e.,

(y₂ − y₁)/(x₂ − x₁) = (y₃ − y₂)/(x₃ − x₂)

Alternatively, they satisfy the area of triangle formula: If area = 0, then points are collinear.

Area of a Triangle

The area of a triangle formed by the vertices A(x₁, y₁), B(x₂, y₂), and C(x₃, y₃) is:

Area = ½ [x₁(y₂ − y₃) + x₂(y₃ − y₁) + x₃(y₁ − y₂)]

If the result is negative, take the absolute value.

Key Points to Remember

1. Distance formula is used to find the length of line segments.
2. Section formula helps find a point dividing a line segment internally.
3. Midpoint formula is a special case of section formula.
4. Area formula can be used to check collinearity of three points (if area = 0).

If the area of the triangle formed by three points is zero, the points are collinear.

Frequently Asked Questions (FAQs) on Coordinate Geometry Case Study